Grafik eksponen adalah salah satu konsep penting dalam matematika yang sering muncul dalam berbagai bidang studi, termasuk ilmu ekonomi, sains, dan teknik. Dalam kehidupan sehari-hari, kita sering melihat fenomena yang mengikuti pola pertumbuhan atau peluruhan eksponensial, seperti penyebaran virus, pertumbuhan populasi, atau perhitungan bunga bank. Namun, banyak orang masih merasa kesulitan memahami bagaimana cara membaca dan memahami grafik eksponen.
Grafik eksponen memiliki bentuk kurva yang unik, yaitu berupa garis lengkung yang naik atau turun secara cepat tergantung pada nilai pangkatnya. Berbeda dengan grafik linear yang memiliki kemiringan tetap, grafik eksponen menunjukkan perubahan yang semakin cepat seiring dengan peningkatan nilai x. Oleh karena itu, memahami grafik eksponen sangat penting untuk bisa menganalisis data yang mengikuti pola pertumbuhan atau peluruhan eksponensial.
Dalam artikel ini, kita akan membahas secara mendalam tentang pengertian grafik eksponen, bagaimana cara membacanya, serta contoh-contoh nyata yang dapat ditemukan dalam kehidupan sehari-hari. Selain itu, kita juga akan menjelaskan sifat-sifat utama dari grafik eksponen dan bagaimana membedakan antara grafik eksponen yang naik dan yang turun.
Apa Itu Grafik Eksponen?
Grafik eksponen adalah representasi visual dari fungsi eksponen. Fungsi eksponen adalah suatu fungsi yang memiliki bentuk umum $ f(x) = a^x $, di mana $ a $ adalah bilangan real positif (disebut basis) dan $ x $ adalah variabel yang berada di pangkat. Contoh sederhana dari fungsi eksponen adalah $ f(x) = 2^x $, $ f(x) = 3^x $, atau $ f(x) = \left(\frac{1}{2}\right)^x $.
Grafik eksponen dibentuk dengan memplot titik-titik koordinat $ (x, f(x)) $ pada bidang Kartesius. Setiap titik yang dipilih akan memberikan informasi tentang bagaimana fungsi tersebut berkembang seiring dengan perubahan nilai $ x $. Karena sifat eksponen yang khas, grafiknya tidak akan berbentuk lurus seperti grafik linear, melainkan berupa kurva yang melengkung.
Beberapa hal yang perlu diketahui tentang grafik eksponen:
- Bentuk Grafik: Grafik eksponen selalu berbentuk kurva yang mulus, bukan garis lurus.
- Posisi Kurva: Grafik eksponen selalu berada di atas sumbu-x (positif) karena nilai $ a^x $ selalu positif untuk semua $ x $.
- Asimtot Horizontal: Grafik eksponen memiliki asimtot horizontal di $ y = 0 $, artinya grafik tidak pernah menyentuh sumbu-x.
- Kemiringan Kurva: Kemiringan grafik eksponen bergantung pada nilai basis $ a $:
- Jika $ a > 1 $, grafik akan naik secara eksponensial.
- Jika $ 0 < a < 1 $, grafik akan turun secara eksponensial.
Sifat-Sifat Utama Grafik Eksponen
Berikut adalah beberapa sifat utama dari grafik eksponen yang perlu Anda pahami:
1. Grafik Selalu Berada di Atas Sumbu-x
Nilai $ a^x $ selalu positif untuk semua $ x $, baik $ x $ positif maupun negatif. Hal ini membuat grafik eksponen selalu berada di atas sumbu-x. Tidak ada titik koordinat yang bernilai negatif pada grafik eksponen.
2. Memotong Sumbu-y di Titik (0, 1)
Jika $ x = 0 $, maka $ a^0 = 1 $ untuk semua $ a \neq 0 $. Artinya, setiap grafik eksponen pasti melewati titik $ (0, 1) $.
3. Memiliki Asimtot Horizontal
Grafik eksponen memiliki asimtot horizontal di $ y = 0 $, yang berarti grafik tidak pernah menyentuh sumbu-x. Meskipun grafik mendekati sumbu-x, ia tidak akan pernah menyentuhnya.
4. Monoton Naik atau Turun
- Monoton Naik: Jika $ a > 1 $, grafik eksponen akan naik secara eksponensial. Semakin besar nilai $ x $, semakin tinggi nilai $ f(x) $.
- Monoton Turun: Jika $ 0 < a < 1 $, grafik eksponen akan turun secara eksponensial. Semakin besar nilai $ x $, semakin kecil nilai $ f(x) $.
5. Simetri dan Perubahan Skala
Grafik eksponen memiliki sifat simetri tertentu jika dilihat dari sudut pandang transformasi fungsi. Misalnya, jika fungsi eksponen diubah menjadi $ f(x) = a^{-x} $, maka grafik akan menjadi cermin dari grafik awalnya.
Cara Membaca Grafik Eksponen
Membaca grafik eksponen tidaklah sulit, asalkan Anda memahami beberapa langkah dasar. Berikut adalah cara-cara membaca grafik eksponen:
1. Identifikasi Basis
Langkah pertama dalam membaca grafik eksponen adalah menentukan nilai basis $ a $. Basis ini menentukan apakah grafik akan naik atau turun:
– Jika $ a > 1 $, grafik akan naik.
– Jika $ 0 < a < 1 $, grafik akan turun.
2. Cari Titik Potong Sumbu-y
Setiap grafik eksponen pasti melewati titik $ (0, 1) $, karena $ a^0 = 1 $. Titik ini bisa menjadi acuan untuk memahami bentuk grafik.
3. Perhatikan Bentuk Kurva
- Grafik Naik: Jika grafik meningkat secara cepat seiring dengan peningkatan nilai $ x $, maka ini adalah grafik eksponen dengan basis $ a > 1 $.
- Grafik Turun: Jika grafik menurun secara cepat seiring dengan peningkatan nilai $ x $, maka ini adalah grafik eksponen dengan basis $ 0 < a < 1 $.
4. Amati Asimtot
Asimtot horizontal di $ y = 0 $ adalah ciri khas dari grafik eksponen. Meskipun grafik mendekati sumbu-x, ia tidak akan pernah menyentuhnya.
5. Bandingkan dengan Grafik Linear
Grafik eksponen berbeda dengan grafik linear karena memiliki bentuk kurva yang semakin curam seiring dengan peningkatan nilai $ x $. Grafik linear memiliki kemiringan tetap, sedangkan grafik eksponen memiliki kemiringan yang meningkat atau menurun secara eksponensial.
Contoh Grafik Eksponen
Untuk lebih memahami cara membaca grafik eksponen, mari kita lihat contoh grafik dari fungsi $ f(x) = 2^x $ dan $ f(x) = \left(\frac{1}{2}\right)^x $.
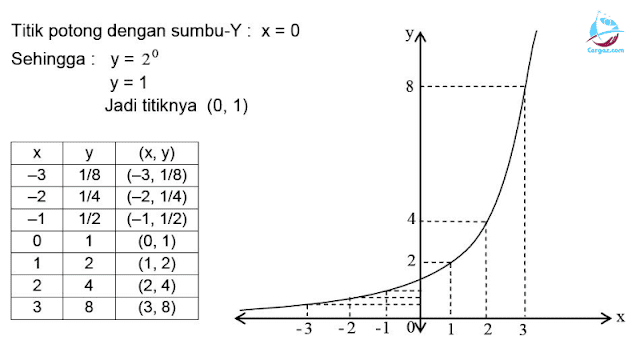
1. Grafik $ f(x) = 2^x $
- Titik-Titik Koordinat:
- $ x = -2 $, $ f(x) = 2^{-2} = \frac{1}{4} $
- $ x = -1 $, $ f(x) = 2^{-1} = \frac{1}{2} $
- $ x = 0 $, $ f(x) = 2^{0} = 1 $
- $ x = 1 $, $ f(x) = 2^{1} = 2 $
-
$ x = 2 $, $ f(x) = 2^{2} = 4 $
-
Ciri-Ciri Grafik:
- Grafik naik secara eksponensial.
- Memotong sumbu-y di titik $ (0, 1) $.
- Memiliki asimtot horizontal di $ y = 0 $.
2. Grafik $ f(x) = \left(\frac{1}{2}\right)^x $
- Titik-Titik Koordinat:
- $ x = -2 $, $ f(x) = \left(\frac{1}{2}\right)^{-2} = 4 $
- $ x = -1 $, $ f(x) = \left(\frac{1}{2}\right)^{-1} = 2 $
- $ x = 0 $, $ f(x) = \left(\frac{1}{2}\right)^{0} = 1 $
- $ x = 1 $, $ f(x) = \left(\frac{1}{2}\right)^{1} = \frac{1}{2} $
-
$ x = 2 $, $ f(x) = \left(\frac{1}{2}\right)^{2} = \frac{1}{4} $
-
Ciri-Ciri Grafik:
- Grafik turun secara eksponensial.
- Memotong sumbu-y di titik $ (0, 1) $.
- Memiliki asimtot horizontal di $ y = 0 $.
Penerapan Grafik Eksponen dalam Kehidupan Nyata
Grafik eksponen tidak hanya digunakan dalam matematika, tetapi juga dalam berbagai bidang kehidupan nyata. Berikut adalah beberapa contoh penerapan grafik eksponen:
1. Pertumbuhan Populasi
Populasi manusia, hewan, atau mikroba sering kali tumbuh secara eksponensial. Contohnya, jika suatu populasi bertambah 10% setiap tahun, maka jumlah populasi akan meningkat secara eksponensial.
2. Penyebaran Virus
Penyebaran virus seperti corona atau flu biasanya mengikuti pola pertumbuhan eksponensial. Dalam waktu singkat, jumlah kasus bisa melonjak drastis.
3. Bunga Bank
Bunga bank yang diberikan oleh bank biasanya dihitung dengan sistem bunga majemuk, yang merupakan contoh lain dari pertumbuhan eksponensial.
4. Peluruhan Radioaktif
Peluruhan radioaktif dari suatu zat radioaktif juga mengikuti pola eksponensial. Jumlah zat radioaktif yang tersisa akan berkurang secara eksponensial seiring waktu.
Kesimpulan
Grafik eksponen adalah representasi visual dari fungsi eksponen yang memiliki bentuk kurva yang unik. Dengan memahami sifat-sifat grafik eksponen, Anda dapat membaca dan menganalisis data yang mengikuti pola pertumbuhan atau peluruhan eksponensial. Dalam kehidupan nyata, grafik eksponen sering digunakan untuk memodelkan berbagai fenomena alami dan sosial, seperti pertumbuhan populasi, penyebaran virus, bunga bank, dan peluruhan radioaktif.
Dengan mempelajari grafik eksponen, Anda tidak hanya akan memperkuat pemahaman matematika Anda, tetapi juga akan lebih mudah memahami fenomena-fenomena yang terjadi di sekitar kita. Semoga artikel ini membantu Anda dalam memahami grafik eksponen dengan lebih baik.


















Komentar