rumus refleksi terhadap sumbu x dalam matematika

Pahami Rumus Refleksi Terhadap Sumbu X dalam Matematika

Refleksi adalah salah satu konsep penting dalam geometri yang sering digunakan dalam berbagai bidang studi, termasuk matematika. Dalam konteks transformasi geometri, refleksi mengacu pada proses pencerminan suatu objek terhadap garis tertentu, seperti sumbu X atau sumbu Y. Salah satu bentuk refleksi yang paling umum adalah refleksi terhadap sumbu X. Konsep ini tidak hanya membantu dalam memahami sifat-sifat geometris tetapi juga memiliki aplikasi praktis dalam berbagai bidang, mulai dari seni hingga teknik.

Dalam artikel ini, kita akan membahas secara mendalam tentang rumus refleksi terhadap sumbu X, termasuk bagaimana cara menerapkannya, sifat-sifatnya, dan contoh soal yang bisa membantu Anda memahami konsep ini lebih baik. Selain itu, kita juga akan menjelaskan perbedaan antara refleksi dengan transformasi lain seperti rotasi dan translasi. Dengan penjelasan yang jelas dan contoh nyata, artikel ini dirancang untuk menjadi panduan lengkap bagi siswa, guru, atau siapa pun yang tertarik belajar tentang matematika.

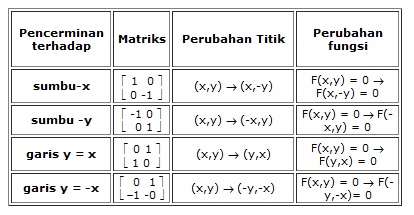
Refleksi terhadap sumbu X adalah transformasi yang memindahkan titik atau objek ke posisi simetris terhadap sumbu X. Artinya, jika sebuah titik memiliki koordinat (x, y), setelah direfleksikan terhadap sumbu X, koordinatnya akan menjadi (x, -y). Proses ini sangat sederhana tetapi memiliki dampak besar dalam memahami hubungan antara titik-titik dalam ruang dua dimensi. Pemahaman tentang konsep ini sangat penting karena sering muncul dalam berbagai soal matematika, khususnya dalam topik transformasi geometri.

Selain itu, refleksi terhadap sumbu X juga memiliki sifat-sifat unik yang membuatnya berbeda dari jenis transformasi lain. Misalnya, jarak antara objek asli dan cermin sama dengan jarak antara bayangan dan cermin. Hal ini menunjukkan bahwa refleksi tidak mengubah ukuran atau bentuk objek, hanya posisinya yang berubah. Pemahaman ini akan sangat berguna ketika Anda ingin menyelesaikan soal-soal yang melibatkan refleksi dan transformasi geometri lainnya.

Apa Itu Refleksi Terhadap Sumbu X?

Refleksi terhadap sumbu X adalah salah satu bentuk transformasi geometri yang paling dasar. Dalam matematika, refleksi didefinisikan sebagai proses pencerminan suatu objek terhadap garis tertentu. Dalam kasus ini, garis tersebut adalah sumbu X, yang merupakan garis horizontal pada bidang Kartesius. Tujuan dari refleksi adalah menciptakan bayangan dari objek asli yang simetris terhadap garis tersebut.

Secara matematis, jika suatu titik memiliki koordinat (x, y), maka hasil refleksi terhadap sumbu X adalah (x, -y). Ini berarti bahwa nilai x tetap sama, sedangkan nilai y berubah tanda. Misalnya, jika titik A memiliki koordinat (2, 3), maka bayangan dari titik A setelah direfleksikan terhadap sumbu X adalah (2, -3). Perubahan ini terjadi karena sumbu X berfungsi sebagai cermin, sehingga posisi vertikal objek dibalik.

Sifat utama dari refleksi terhadap sumbu X adalah bahwa jarak antara objek asli dan sumbu X sama dengan jarak antara bayangan dan sumbu X. Selain itu, garis penghubung antara objek asli dan bayangan selalu tegak lurus terhadap sumbu X. Hal ini menunjukkan bahwa refleksi tidak hanya mengubah posisi objek, tetapi juga mempertahankan bentuk dan ukurannya.

Refleksi terhadap sumbu X memiliki banyak aplikasi dalam kehidupan sehari-hari. Contohnya, pantulan benda di genangan air atau bayangan manusia di permukaan kaca dapat dijelaskan menggunakan konsep ini. Di dunia pendidikan, refleksi terhadap sumbu X sering digunakan dalam pembelajaran geometri untuk membantu siswa memahami sifat-sifat simetri dan transformasi.

Sifat-Sifat Refleksi Terhadap Sumbu X

Refleksi terhadap sumbu X memiliki beberapa sifat penting yang membedakannya dari jenis transformasi lain. Pertama, refleksi tidak mengubah bentuk atau ukuran objek. Bayangan yang dihasilkan memiliki bentuk dan ukuran yang identik dengan objek aslinya, hanya posisinya yang berubah. Sifat ini disebut sebagai isometri, yang berarti transformasi tidak mengubah jarak antara titik-titik dalam objek.

Kedua, jarak antara objek asli dan sumbu X sama dengan jarak antara bayangan dan sumbu X. Ini berarti bahwa objek dan bayangannya memiliki jarak yang sama terhadap garis cermin. Jika objek berada di atas sumbu X, maka bayangannya akan berada di bawah sumbu X dengan jarak yang sama. Sebaliknya, jika objek berada di bawah sumbu X, bayangannya akan berada di atas sumbu X.

Ketiga, garis penghubung antara objek asli dan bayangan selalu tegak lurus terhadap sumbu X. Artinya, garis yang menghubungkan titik asli dan titik bayangan akan membentuk sudut 90 derajat dengan sumbu X. Hal ini memastikan bahwa refleksi terhadap sumbu X menghasilkan bayangan yang simetris secara vertikal.

Keempat, semua garis penghubung antara objek asli dan bayangan sejajar satu sama lain. Ini berarti bahwa jika ada beberapa titik yang direfleksikan terhadap sumbu X, garis-garis yang menghubungkan titik-titik asli dengan titik-titik bayangan akan saling sejajar. Sifat ini memudahkan analisis dan pemahaman tentang bagaimana objek bergerak saat direfleksikan.

Terakhir, sudut antara sinar datang dan sinar pantul sama besar. Meskipun ini lebih relevan dalam konteks optik, prinsip ini juga berlaku dalam refleksi matematika. Dengan kata lain, sudut yang dibentuk oleh garis yang menghubungkan objek asli dan sumbu X sama dengan sudut yang dibentuk oleh garis yang menghubungkan bayangan dan sumbu X.

Cara Menggunakan Rumus Refleksi Terhadap Sumbu X

Menggunakan rumus refleksi terhadap sumbu X cukup sederhana. Seperti yang telah dijelaskan sebelumnya, jika suatu titik memiliki koordinat (x, y), maka hasil refleksi terhadap sumbu X adalah (x, -y). Untuk menerapkan rumus ini, ikuti langkah-langkah berikut:

1. Identifikasi koordinat titik asli. Misalnya, titik A memiliki koordinat (2, 3).
2. Terapkan rumus refleksi terhadap sumbu X. Nilai x tetap sama, sedangkan nilai y berubah tanda.
3. Hitung koordinat bayangan. Dalam contoh ini, bayangan titik A adalah (2, -3).

Untuk menerapkan rumus ini pada objek yang lebih kompleks, seperti garis atau bangun datar, Anda perlu menerapkan rumus tersebut pada setiap titik yang membentuk objek tersebut. Misalnya, jika Anda memiliki segitiga dengan titik-titik A(2, 3), B(4, 5), dan C(6, 7), maka bayangan dari segitiga tersebut setelah direfleksikan terhadap sumbu X adalah A'(2, -3), B'(4, -5), dan C'(6, -7).

Selain itu, Anda juga dapat menggunakan rumus ini untuk menyelesaikan soal-soal yang melibatkan refleksi terhadap sumbu X. Misalnya, jika Anda diminta untuk menentukan koordinat bayangan dari titik (5, -2) setelah direfleksikan terhadap sumbu X, maka jawabannya adalah (5, 2). Dengan memahami cara menerapkan rumus ini, Anda dapat menyelesaikan berbagai jenis soal yang berkaitan dengan refleksi terhadap sumbu X.

Contoh Soal dan Pembahasan

Berikut adalah beberapa contoh soal yang melibatkan refleksi terhadap sumbu X beserta penjelasan langkah-langkah penyelesaiannya:

Contoh 1:

Titik A(2, 3) direfleksikan terhadap sumbu X. Tentukan koordinat bayangan titik A.

Penyelesaian:

Rumus refleksi terhadap sumbu X adalah (x, y) → (x, -y).

Maka, koordinat bayangan titik A adalah (2, -3).

Contoh 2:

Titik B(-4, 5) direfleksikan terhadap sumbu X. Tentukan koordinat bayangan titik B.

Penyelesaian:

Rumus refleksi terhadap sumbu X adalah (x, y) → (x, -y).

Maka, koordinat bayangan titik B adalah (-4, -5).

Contoh 3:

Titik C(1, -2) direfleksikan terhadap sumbu X. Tentukan koordinat bayangan titik C.

Penyelesaian:

Rumus refleksi terhadap sumbu X adalah (x, y) → (x, -y).

Maka, koordinat bayangan titik C adalah (1, 2).

Contoh 4:

Garis y = 2x + 1 direfleksikan terhadap sumbu X. Tentukan persamaan garis hasil refleksi.

Penyelesaian:

Untuk menyelesaikan soal ini, kita perlu mengganti y dengan -y dalam persamaan garis.

Persamaan awal: y = 2x + 1.

Setelah refleksi: -y = 2x + 1 → y = -2x – 1.

Contoh 5:

Lingkaran dengan persamaan x² + y² = 9 direfleksikan terhadap sumbu X. Tentukan persamaan lingkaran hasil refleksi.

Penyelesaian:

Rumus refleksi terhadap sumbu X adalah (x, y) → (x, -y).

Substitusi y dengan -y dalam persamaan lingkaran: x² + (-y)² = 9 → x² + y² = 9.

Jadi, persamaan lingkaran hasil refleksi tetap sama, yaitu x² + y² = 9.

Dengan memahami cara menerapkan rumus refleksi terhadap sumbu X, Anda dapat menyelesaikan berbagai jenis soal yang melibatkan transformasi geometri ini.

Perbedaan Antara Refleksi, Rotasi, dan Translasi

Refleksi, rotasi, dan translasi adalah tiga jenis transformasi geometri yang sering digunakan dalam matematika. Meskipun ketiganya mengubah posisi objek, masing-masing memiliki karakteristik dan sifat yang berbeda. Berikut adalah perbedaan utama antara ketiganya:

1. Refleksi:
   
   Refleksi adalah proses pencerminan suatu objek terhadap garis tertentu, seperti sumbu X atau sumbu Y. Hasil dari refleksi adalah bayangan yang simetris terhadap garis tersebut. Refleksi tidak mengubah bentuk atau ukuran objek, hanya posisinya yang berubah. Contohnya, bayangan manusia di cermin datar adalah hasil refleksi terhadap cermin tersebut.

2. Rotasi:
   
   Rotasi adalah perubahan posisi suatu objek dengan cara memutarnya sebesar sudut tertentu mengelilingi titik pusat. Rotasi menghasilkan bayangan yang berjarak sama dengan objek dari pusat rotasi dan membentuk sudut yang sama dengan sudut rotasi. Contohnya, jarum jam yang berputar adalah hasil rotasi terhadap titik pusat jam.

3. Translasi:
   
   Translasi adalah perubahan posisi suatu objek dengan cara menggesernya sejauh dan searah vektor tertentu. Translasi menghasilkan bayangan yang sejajar dan kongruen dengan objek. Contohnya, mobil yang bergerak di jalan lurus adalah hasil translasi terhadap vektor arah dan jarak perpindahan mobil.

Perbedaan utama antara ketiganya adalah bahwa refleksi menghasilkan bayangan simetris, rotasi menghasilkan bayangan yang diputar, dan translasi menghasilkan bayangan yang digeser. Memahami perbedaan ini sangat penting dalam menyelesaikan soal-soal yang melibatkan transformasi geometri.

Penerapan Rumus Refleksi Terhadap Sumbu X dalam Kehidupan Nyata

Meskipun rumus refleksi terhadap sumbu X terlihat sederhana, konsep ini memiliki banyak penerapan dalam kehidupan nyata. Beberapa contoh penerapan ini meliputi:

1. Pantulan di Genangan Air:
   
   Saat hujan turun, genangan air di jalan dapat menjadi cermin alami yang memantulkan bayangan benda-benda di sekitarnya. Bayangan ini dapat dijelaskan menggunakan konsep refleksi terhadap sumbu X, terutama jika genangan air berada di permukaan horizontal.

2. Cermin Datar:
   
   Cermin datar adalah contoh nyata dari refleksi. Bayangan yang terbentuk di cermin adalah hasil dari pencerminan objek terhadap permukaan cermin. Dalam hal ini, jika objek berada di atas cermin, bayangannya akan berada di bawah cermin dengan jarak yang sama.

3. Desain Grafis dan Seni:
   
   Dalam desain grafis dan seni, konsep refleksi digunakan untuk menciptakan efek simetri dan keseimbangan. Misalnya, ilustrasi yang memiliki elemen simetris dapat dihasilkan dengan menerapkan refleksi terhadap sumbu X atau Y.

4. Pengambilan Foto dan Video:
   
   Dalam fotografi dan video, refleksi sering digunakan untuk menciptakan efek visual yang menarik. Contohnya, foto yang menampilkan pantulan benda di permukaan air atau kaca dapat dihasilkan dengan memanfaatkan prinsip refleksi terhadap sumbu X.

5. Pendidikan Matematika:
   
   Di sekolah, refleksi terhadap sumbu X sering digunakan dalam pembelajaran geometri untuk membantu siswa memahami sifat-sifat simetri dan transformasi. Dengan memahami konsep ini, siswa dapat menyelesaikan berbagai jenis soal yang melibatkan refleksi dan transformasi lainnya.

Dengan demikian, rumus refleksi terhadap sumbu X tidak hanya berguna dalam matematika, tetapi juga memiliki aplikasi nyata dalam berbagai bidang. Pemahaman tentang konsep ini sangat penting bagi siapa saja yang ingin memahami lebih dalam tentang transformasi geometri dan sifat-sifatnya.