Fungsi kuadrat adalah salah satu konsep penting dalam matematika yang sering muncul dalam berbagai bidang, termasuk fisika, ekonomi, dan teknik. Dalam artikel ini, kita akan membahas secara lengkap mengenai rumus fungsi kuadrat, bagaimana menggambar grafiknya, serta contoh soal untuk memperdalam pemahaman.
Apa Itu Fungsi Kuadrat?
Fungsi kuadrat adalah fungsi matematika yang memiliki bentuk umum:
$$
f(x) = ax^2 + bx + c
$$
di mana $ a $, $ b $, dan $ c $ adalah konstanta, dan $ a \neq 0 $. Grafik dari fungsi kuadrat selalu berbentuk parabola. Parabola dapat terbuka ke atas jika $ a > 0 $, atau ke bawah jika $ a < 0 $.
Sifat-Sifat Fungsi Kuadrat
- Titik Puncak (Vertex): Titik tertinggi atau terendah pada parabola.
- Sumbu Simetri: Garis vertikal yang membagi parabola menjadi dua bagian simetris.
- Titik Potong Sumbu X: Akar-akar persamaan kuadrat.
- Titik Potong Sumbu Y: Nilai fungsi ketika $ x = 0 $.
Rumus Fungsi Kuadrat
Bentuk umum fungsi kuadrat adalah:
$$
f(x) = ax^2 + bx + c
$$
Dari bentuk ini, kita dapat menentukan beberapa hal penting seperti:
– Koordinat titik puncak:
$$
x_p = -\frac{b}{2a}, \quad y_p = f(x_p)
$$
– Diskriminan:
$$
D = b^2 – 4ac
$$
Diskriminan digunakan untuk menentukan jenis akar dari fungsi kuadrat:
– Jika $ D > 0 $: dua akar real berbeda.
– Jika $ D = 0 $: satu akar real (ganda).
– Jika $ D < 0 $: tidak ada akar real (akar kompleks).
Cara Menggambar Grafik Fungsi Kuadrat
Untuk menggambar grafik fungsi kuadrat, ikuti langkah-langkah berikut:
- Tentukan koefisien $ a $, $ b $, dan $ c $.
- Cari titik puncak menggunakan rumus $ x_p = -\frac{b}{2a} $, lalu substitusi ke fungsi untuk mendapatkan $ y_p $.
- Cari titik potong sumbu X dengan mencari akar-akar persamaan kuadrat $ f(x) = 0 $.
- Cari titik potong sumbu Y dengan substitusi $ x = 0 $.
- Plot titik-titik tersebut dan hubungkan dengan kurva parabola.
Contoh: Untuk fungsi $ f(x) = x^2 – 4x + 3 $,
– Titik puncak: $ x = 2 $, $ f(2) = -1 $
– Titik potong sumbu X: $ x = 1 $ dan $ x = 3 $
– Titik potong sumbu Y: $ y = 3 $
Contoh Soal Fungsi Kuadrat
Soal:
Diketahui fungsi $ f(x) = x^2 – 4x + 3 $. Gambar grafiknya dan tentukan titik puncak serta titik potongnya.
Penyelesaian:
- Identifikasi koefisien:
- $ a = 1 $, $ b = -4 $, $ c = 3 $
- Cari titik puncak:
$$
x_p = -\frac{-4}{2 \cdot 1} = 2, \quad f(2) = 2^2 – 4 \cdot 2 + 3 = -1
$$
Jadi, titik puncaknya adalah $ (2, -1) $. - Cari titik potong sumbu X:
$$
x^2 – 4x + 3 = 0 \Rightarrow (x – 1)(x – 3) = 0 \Rightarrow x = 1, 3
$$
Jadi, titik potongnya adalah $ (1, 0) $ dan $ (3, 0) $. - Cari titik potong sumbu Y:
$$
f(0) = 0^2 – 4 \cdot 0 + 3 = 3
$$
Jadi, titik potongnya adalah $ (0, 3) $.
Tips Belajar Fungsi Kuadrat
- Latihan soal sebanyak mungkin untuk memahami pola parabola.
- Gunakan kertas grafik untuk memvisualisasikan kurva.
- Pahami hubungan antara koefisien $ a $, $ b $, dan $ c $ dengan bentuk grafik.
Kesimpulan
Grafik fungsi kuadrat adalah alat penting dalam matematika yang membantu memvisualisasikan hubungan antar variabel. Dengan memahami rumus, langkah menggambar, dan latihan soal, kamu bisa menguasai materi ini dengan mudah. Yuk, coba kerjakan lebih banyak soal untuk memperdalam pemahamanmu!
Jika kamu ingin mempelajari lebih lanjut tentang fungsi kuadrat, kamu juga bisa mempelajari cara menyelesaikan persamaan kuadrat, menentukan nilai optimum, atau memahami aplikasi fungsi kuadrat dalam kehidupan nyata. Semangat belajar!



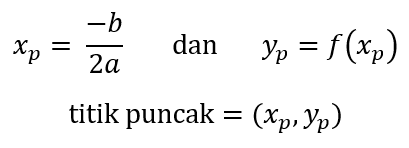















Komentar