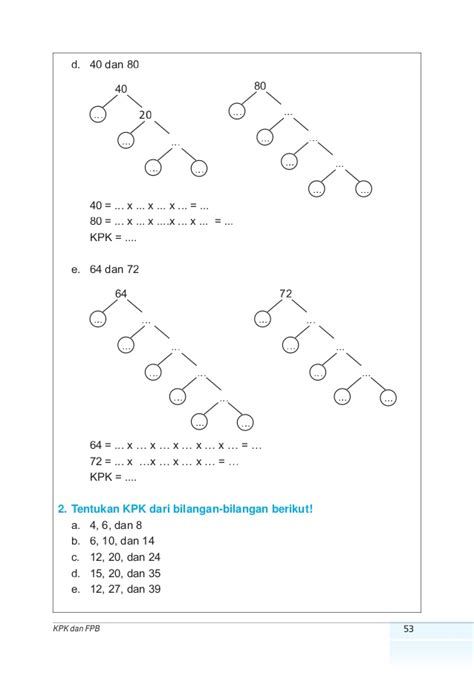
Pohon Faktor: Pengertian, Manfaat, dan Cara Membuatnya

Pohon faktor adalah salah satu konsep penting dalam matematika yang digunakan untuk memahami struktur bilangan. Dengan menggunakan pohon faktor, kita dapat menguraikan suatu bilangan menjadi faktor-faktornya, terutama faktor prima. Konsep ini sangat berguna dalam berbagai bidang seperti kriptografi, algoritma komputer, dan pemecahan masalah matematika lainnya. Pohon faktor tidak hanya membantu siswa dalam belajar matematika, tetapi juga menjadi alat bantu bagi para peneliti dan pengembang teknologi.

Pohon faktor diperkenalkan sebagai metode visual untuk menemukan faktorisasi prima dari suatu bilangan. Dalam pohon faktor, setiap cabang merepresentasikan pembagian bilangan dengan faktor prima. Proses ini dimulai dari bilangan utama yang ingin dipecah, lalu dibagi dengan bilangan prima terkecil hingga semua hasilnya adalah bilangan prima. Dengan demikian, pohon faktor memberikan gambaran jelas tentang bagaimana suatu bilangan terbentuk dari perkalian bilangan-bilangan prima.

Manfaat pohon faktor tidak hanya terbatas pada pendidikan matematika. Dalam kehidupan sehari-hari, pohon faktor digunakan untuk menyelesaikan masalah seperti mencari Kelipatan Persekutuan Terkecil (KPK) dan Faktor Persekutuan Terbesar (FPB). Selain itu, pohon faktor juga menjadi dasar dalam beberapa algoritma komputasi modern, termasuk enkripsi data. Oleh karena itu, memahami pohon faktor sangat penting bagi siapa pun yang tertarik dalam matematika atau teknologi informasi.

Apa Itu Pohon Faktor?

Pohon faktor adalah representasi visual dari proses faktorisasi prima suatu bilangan. Dalam pohon faktor, bilangan awal ditempatkan di bagian atas, kemudian dibagi dengan faktor prima terkecil. Setiap pembagian menghasilkan dua cabang: satu untuk faktor yang dipilih dan satu untuk hasil pembagian. Proses ini dilanjutkan hingga semua angka yang tersisa adalah bilangan prima.

Contohnya, mari kita lihat pohon faktor dari bilangan 36. Kita mulai dengan 36 di bagian atas. Karena 36 habis dibagi 2, kita tulis 2 dan 18. Lalu, 18 juga habis dibagi 2, sehingga kita tulis 2 dan 9. Angka 9 tidak habis dibagi 2, maka kita coba dengan 3. Hasilnya adalah 3 dan 3. Akhirnya, semua angka yang tersisa adalah bilangan prima, yaitu 2, 2, 3, dan 3. Jadi, faktorisasi prima dari 36 adalah 2 × 2 × 3 × 3 atau 2² × 3².

Pohon faktor memiliki bentuk yang mirip dengan pohon nyata, dengan akar di bagian atas dan cabang-cabang yang menyebar ke bawah. Setiap cabang mewakili proses pembagian, sementara daun-daunnya adalah bilangan prima yang merupakan faktor dari bilangan awal.

Manfaat Pohon Faktor

Pohon faktor memiliki banyak manfaat, baik dalam pendidikan maupun dalam penerapan praktis. Berikut beberapa manfaat utamanya:

1. Membantu Siswa Memahami Faktorisasi Prima
   
   Pohon faktor memberikan cara visual yang mudah dipahami oleh siswa untuk memahami bagaimana suatu bilangan terbentuk dari perkalian bilangan-bilangan prima. Dengan melihat pohon faktor, siswa bisa lebih mudah mengidentifikasi faktor-faktor prima dari suatu bilangan.

2. Mencari Faktor Persekutuan Terbesar (FPB)
   
   FPB dari dua bilangan dapat ditemukan dengan membandingkan faktor-faktor prima dari kedua bilangan tersebut. Pohon faktor membantu mengidentifikasi faktor-faktor prima yang sama, sehingga mempermudah perhitungan FPB.

3. Mencari Kelipatan Persekutuan Terkecil (KPK)
   
   KPK dari dua bilangan dapat ditemukan dengan mengalikan semua faktor prima dari kedua bilangan tersebut, termasuk faktor-faktor yang sama. Pohon faktor memberikan pandangan yang jelas tentang faktor-faktor yang diperlukan untuk menghitung KPK.

   Read also: Apa Itu Bagian Keuangan dan Fungsi Utamanya dalam Perusahaan?

4. Mengoptimalkan Algoritma Komputer
   
   Dalam dunia komputer, pohon faktor digunakan sebagai dasar dalam algoritma pencarian faktor prima. Pohon faktor membantu mempercepat proses pencarian faktor prima dengan membagi bilangan menjadi bagian-bagian yang lebih kecil.

5. Meningkatkan Kemampuan Logika dan Analisis
   
   Menggunakan pohon faktor melibatkan logika dan analisis, yang membantu meningkatkan kemampuan berpikir kritis siswa. Dengan latihan berulang, siswa akan lebih mahir dalam memecahkan masalah matematika yang kompleks.

Cara Membuat Pohon Faktor

Membuat pohon faktor cukup sederhana, tetapi memerlukan kesabaran dan ketelitian. Berikut langkah-langkahnya:

1. Tulis Bilangan Awal di Bagian Atas
   
   Mulailah dengan menulis bilangan yang ingin Anda faktorkan di bagian atas pohon faktor. Misalnya, jika ingin mencari faktor dari 48, tuliskan 48 di bagian atas.

2. Bagi dengan Bilangan Prima Terkecil
   
   Cari bilangan prima terkecil yang dapat membagi bilangan awal tanpa menyisakan sisa. Contohnya, 48 dapat dibagi dengan 2, karena 48 ÷ 2 = 24.

   Read also: Pengertian dan Cara Mencari Refleksi Terhadap Sumbu X dalam Matematika

3. Tulis Hasil Pembagian dan Faktor
   
   Tuliskan hasil pembagian (24) dan faktor (2) sebagai dua cabang dari bilangan awal. Sekarang, pohon faktor memiliki dua cabang: 2 dan 24.

4. Ulangi Proses untuk Setiap Cabang
   
   Ulangi langkah 2 dan 3 untuk setiap cabang. Misalnya, 24 dapat dibagi dengan 2, sehingga kita tulis 2 dan 12. Lalu, 12 dapat dibagi dengan 2 lagi, menghasilkan 2 dan 6. Proses ini dilanjutkan hingga semua angka yang tersisa adalah bilangan prima.

5. Identifikasi Faktor Prima
   
   Setelah semua cabang telah dibagi hingga mendapatkan bilangan prima, identifikasi semua faktor prima yang ada. Untuk contoh 48, faktor primanya adalah 2, 2, 2, 2, dan 3.

6. Tulis Faktorisasi Prima
   
   Setelah semua faktor prima diketahui, tuliskan hasilnya dalam bentuk perkalian. Untuk 48, faktorisasi primanya adalah 2 × 2 × 2 × 2 × 3 atau 2⁴ × 3.

Dengan mengikuti langkah-langkah di atas, Anda dapat membuat pohon faktor sendiri. Proses ini tidak hanya membantu dalam memahami matematika, tetapi juga meningkatkan keterampilan analitis dan logika.

Pohon Faktor dalam Pendidikan Matematika

Pohon faktor menjadi alat yang sangat berguna dalam pendidikan matematika, terutama untuk siswa SD dan SMP. Di tingkat sekolah dasar, siswa diajarkan tentang bilangan prima dan cara memfaktorkan bilangan. Pohon faktor memberikan cara visual yang mudah dipahami, sehingga siswa bisa belajar secara interaktif.

Selain itu, pohon faktor juga digunakan dalam materi KPK dan FPB. Dengan pohon faktor, siswa bisa melihat bagaimana faktor-faktor prima dari dua bilangan berbeda, sehingga mereka bisa menemukan KPK dan FPB dengan lebih cepat dan akurat.

Di tingkat sekolah menengah, pohon faktor digunakan sebagai dasar dalam memahami konsep-konsep matematika yang lebih kompleks, seperti teori bilangan dan algoritma. Siswa yang memahami pohon faktor akan lebih mudah memahami topik-topik seperti kriptografi dan enkripsi data.

Pohon Faktor dalam Teknologi Informasi

Di dunia teknologi informasi, pohon faktor memiliki peran penting dalam berbagai aplikasi. Salah satunya adalah dalam kriptografi, di mana bilangan prima digunakan untuk mengenkripsi dan mendekripsi pesan. Proses enkripsi ini melibatkan penggunaan bilangan besar yang terbentuk dari perkalian dua bilangan prima. Namun, memecahkan bilangan tersebut kembali menjadi dua bilangan prima asli sangat sulit, bahkan untuk komputer modern sekalipun.

Pohon faktor digunakan sebagai alat bantu dalam proses pencarian faktor prima. Dengan membagi bilangan menjadi bagian-bagian yang lebih kecil, proses pencarian faktor prima menjadi lebih efisien. Dalam industri keamanan digital, pohon faktor menjadi salah satu alat yang digunakan untuk memastikan keamanan data.

Selain itu, pohon faktor juga digunakan dalam algoritma pencarian dan pengurutan. Dalam algoritma seperti QuickSort dan MergeSort, pohon faktor membantu membagi data menjadi bagian-bagian yang lebih kecil, sehingga proses pengurutan menjadi lebih cepat dan efisien.

Kelebihan dan Kekurangan Pohon Faktor

Meskipun pohon faktor memiliki banyak manfaat, ada juga kelebihan dan kekurangan yang perlu diperhatikan:

Kelebihan:
– Visual dan Mudah Dipahami: Pohon faktor memberikan representasi visual yang jelas, sehingga lebih mudah dipahami oleh siswa.
– Meningkatkan Kemampuan Logika: Proses pembuatan pohon faktor melibatkan logika dan analisis, yang membantu meningkatkan kemampuan berpikir kritis.
– Membantu dalam KPK dan FPB: Pohon faktor memberikan cara yang efektif untuk mencari KPK dan FPB dari dua bilangan.

Kekurangan:
– Waktu dan Kesabaran: Membuat pohon faktor membutuhkan waktu dan kesabaran, terutama untuk bilangan besar.
– Tidak Efisien untuk Bilangan Besar: Untuk bilangan yang sangat besar, proses pembuatan pohon faktor menjadi sangat lambat dan tidak efisien.
– Memerlukan Pengetahuan Dasar tentang Bilangan Prima: Tanpa pemahaman dasar tentang bilangan prima, pohon faktor tidak akan efektif.

Tips untuk Membuat Pohon Faktor yang Efisien

Untuk membuat pohon faktor yang efisien, berikut beberapa tips yang bisa Anda ikuti:

1. Mulai dengan Bilangan Prima Terkecil
   
   Selalu mulai dengan bilangan prima terkecil, seperti 2, 3, 5, dan seterusnya. Ini akan mempercepat proses pembagian dan menghindari pembagian yang tidak perlu.

2. Gunakan Kalkulator atau Aplikasi Bantu
   
   Jika Anda menghadapi bilangan besar, gunakan kalkulator atau aplikasi bantu untuk mempercepat proses. Banyak kalkulator online yang bisa membantu Anda membuat pohon faktor secara otomatis.

3. Latih Kemampuan Berpikir Logis
   
   Latih kemampuan berpikir logis dengan mencoba membuat pohon faktor sendiri. Semakin sering Anda berlatih, semakin cepat dan akurat Anda dalam membuat pohon faktor.

4. Gunakan Metode Alternatif
   
   Jika pohon faktor terlalu rumit, coba metode alternatif seperti pembagian percobaan atau metode faktorisasi lainnya. Metode ini bisa lebih cepat untuk bilangan tertentu.

5. Cari Pola dalam Faktor Prima
   
   Beberapa bilangan memiliki pola dalam faktor primanya. Dengan mengenali pola ini, Anda bisa membuat pohon faktor dengan lebih cepat dan efisien.

Kesimpulan

Pohon faktor adalah alat penting dalam matematika yang membantu memahami struktur bilangan. Dengan pohon faktor, kita bisa menguraikan suatu bilangan menjadi faktor-faktornya, terutama faktor prima. Pohon faktor memiliki banyak manfaat, baik dalam pendidikan maupun dalam penerapan praktis seperti kriptografi dan algoritma komputer.

Meskipun pohon faktor memiliki kelebihan seperti visual yang jelas dan kemampuan meningkatkan logika, ia juga memiliki kekurangan seperti membutuhkan waktu dan kesabaran. Namun, dengan latihan dan pengetahuan dasar tentang bilangan prima, Anda bisa membuat pohon faktor dengan lebih efisien.

Jika Anda tertarik mempelajari pohon faktor lebih lanjut, cobalah menggunakan kalkulator online atau aplikasi bantu yang tersedia. Dengan alat-alat ini, Anda bisa membuat pohon faktor secara otomatis dan memahami konsep ini dengan lebih mudah.