Persamaan garis singgung lingkaran adalah salah satu konsep penting dalam geometri yang sering muncul dalam pelajaran matematika. Dalam kehidupan sehari-hari, kita sering melihat bentuk lingkaran seperti roda kendaraan, jam dinding, atau benda-benda lainnya. Namun, ketika kita mempelajari matematika, terutama di tingkat SMA, kita akan menemui berbagai masalah terkait dengan garis singgung lingkaran.
Garis singgung lingkaran adalah garis yang hanya menyentuh lingkaran di satu titik. Dalam konteks matematika, garis ini memiliki hubungan khusus dengan lingkaran, yaitu gradien garis tersebut harus sesuai dengan kondisi tertentu agar bisa menyinggung lingkaran. Oleh karena itu, memahami cara menentukan persamaan garis singgung lingkaran sangat penting untuk menyelesaikan soal-soal yang berkaitan.
Dalam artikel ini, kita akan membahas secara rinci tentang persamaan garis singgung lingkaran, termasuk bagaimana menentukannya jika diketahui gradien garis singgung dan persamaan lingkaran. Kita juga akan memberikan contoh soal beserta penyelesaiannya agar kamu dapat lebih mudah memahami konsep ini.
Apa Itu Garis Singgung Lingkaran?
Sebelum kita membahas lebih jauh, mari kita pahami dulu apa itu garis singgung lingkaran. Secara sederhana, garis singgung adalah garis yang hanya menyentuh lingkaran di satu titik. Tidak seperti garis potong yang memotong lingkaran di dua titik, garis singgung hanya bersinggungan di satu titik.
Dalam geometri, setiap lingkaran memiliki tak hingga jumlah garis singgung. Namun, jika kita tahu gradien garis singgung dan persamaan lingkaran, maka kita dapat menentukan persamaan garis singgung tersebut. Hal ini sangat berguna dalam berbagai bidang, seperti teknik, fisika, dan matematika lanjutan.
Rumus Dasar Persamaan Garis Singgung Lingkaran
Untuk menentukan persamaan garis singgung lingkaran, kita perlu mengenal beberapa rumus dasar. Berikut adalah beberapa rumus yang umum digunakan:
-
Lingkaran dengan pusat di titik asal (0, 0)
Jika lingkaran memiliki persamaan $x^2 + y^2 = r^2$, maka persamaan garis singgung dengan gradien $m$ adalah:
$$
y = mx \pm r\sqrt{m^2 + 1}
$$ -
Lingkaran dengan pusat di $(a, b)$
Jika lingkaran memiliki persamaan $(x – a)^2 + (y – b)^2 = r^2$, maka persamaan garis singgung dengan gradien $m$ adalah:
$$
y – b = m(x – a) \pm r\sqrt{m^2 + 1}
$$
Rumus-rumus ini sangat berguna ketika kita ingin menentukan persamaan garis singgung lingkaran jika diketahui gradien garis singgung dan persamaan lingkaran.
Langkah-Langkah Menentukan Persamaan Garis Singgung Lingkaran
Berikut adalah langkah-langkah yang bisa kamu ikuti untuk menentukan persamaan garis singgung lingkaran jika diketahui gradien garis singgung dan persamaan lingkaran:
1. Identifikasi Pusat dan Jari-Jari Lingkaran
Jika persamaan lingkaran sudah diketahui, misalnya $x^2 + y^2 = r^2$, maka pusat lingkaran adalah $(0, 0)$ dan jari-jari adalah $r$. Jika persamaan lingkaran berbentuk $(x – a)^2 + (y – b)^2 = r^2$, maka pusat lingkaran adalah $(a, b)$ dan jari-jari adalah $r$.
2. Tentukan Gradien Garis Singgung
Gradien garis singgung biasanya sudah diketahui dalam soal. Misalnya, gradien garis singgung adalah $m$.
3. Gunakan Rumus Persamaan Garis Singgung
Setelah mengetahui pusat lingkaran, jari-jari, dan gradien garis singgung, gunakan rumus yang sesuai. Misalnya, jika lingkaran berpusat di $(a, b)$ dan gradien garis singgung adalah $m$, maka persamaan garis singgungnya adalah:
$$
y – b = m(x – a) \pm r\sqrt{m^2 + 1}
$$
4. Sederhanakan Persamaan
Setelah mendapatkan persamaan garis singgung, sederhanakan bentuknya agar lebih mudah dibaca dan dipahami.
Contoh Soal dan Penyelesaian
Mari kita lihat contoh soal untuk memperjelas konsep ini.
Contoh Soal 1
Tentukan persamaan garis singgung pada lingkaran $x^2 + y^2 = 10$ dengan gradien $3$.
Penyelesaian:
- Pusat lingkaran: $(0, 0)$
- Jari-jari: $\sqrt{10}$
- Gradien garis singgung: $3$
Gunakan rumus:
$$
y = mx \pm r\sqrt{m^2 + 1}
$$
Substitusi nilai:
$$
y = 3x \pm \sqrt{10} \cdot \sqrt{3^2 + 1} = 3x \pm \sqrt{10} \cdot \sqrt{10} = 3x \pm 10
$$
Jadi, persamaan garis singgungnya adalah $y = 3x + 10$ atau $y = 3x – 10$.
Contoh Soal 2
Tentukan persamaan garis singgung pada lingkaran $(x – 2)^2 + (y + 5)^2 = 20$ dengan gradien $2$.
Penyelesaian:
- Pusat lingkaran: $(2, -5)$
- Jari-jari: $\sqrt{20}$
- Gradien garis singgung: $2$
Gunakan rumus:
$$
y – (-5) = 2(x – 2) \pm \sqrt{20} \cdot \sqrt{2^2 + 1}
$$
Sederhanakan:
$$
y + 5 = 2x – 4 \pm \sqrt{20} \cdot \sqrt{5} = 2x – 4 \pm \sqrt{100} = 2x – 4 \pm 10
$$
Jadi, persamaan garis singgungnya adalah $y = 2x – 9$ atau $y = 2x + 1$.
Tips untuk Memahami Persamaan Garis Singgung Lingkaran
- Pahami Konsep Dasar: Pastikan kamu memahami apa itu lingkaran, pusat lingkaran, dan jari-jari.
- Latihan Soal: Semakin banyak latihan, semakin mudah kamu memahami konsep ini.
- Gunakan Grafik: Menggambar grafik lingkaran dan garis singgung bisa membantu kamu memvisualisasikan posisi garis singgung.
- Konsisten dalam Penggunaan Rumus: Selalu gunakan rumus yang sesuai dengan bentuk persamaan lingkaran yang diberikan.
Kesimpulan
Persamaan garis singgung lingkaran adalah konsep penting dalam matematika yang sering muncul dalam berbagai soal. Dengan memahami rumus dasar dan langkah-langkah penyelesaian, kamu dapat dengan mudah menentukan persamaan garis singgung lingkaran jika diketahui gradien garis singgung dan persamaan lingkaran. Latihan soal dan penggunaan grafik akan membantu kamu memperkuat pemahamanmu. Dengan demikian, kamu tidak lagi merasa bingung saat menghadapi soal-soal yang berkaitan dengan garis singgung lingkaran.





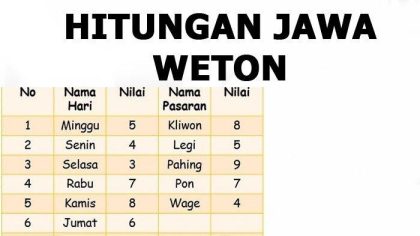
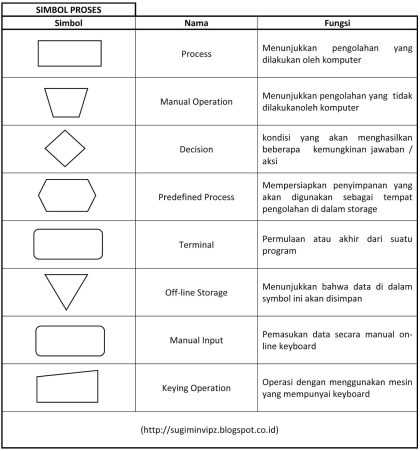













Komentar