Pencerminan adalah salah satu konsep penting dalam ilmu matematika, khususnya dalam bidang geometri. Dalam kehidupan sehari-hari, kita sering melihat fenomena pencerminan, baik itu dari benda-benda fisik seperti cermin, genangan air, atau bahkan bayangan yang terbentuk di bawah sinar matahari. Pencerminan tidak hanya sekadar fenomena visual, tetapi juga memiliki sifat-sifat matematis yang menarik untuk dipelajari. Dengan memahami pencerminan, kita bisa lebih memahami bagaimana objek berubah posisi dan bentuk ketika diterapkan transformasi geometri.
Secara umum, pencerminan dapat diartikan sebagai proses memindahkan titik-titik suatu objek dengan menggunakan sifat bayangan cermin. Bayangan yang dihasilkan memiliki bentuk dan ukuran yang sama dengan objek aslinya, tetapi posisinya berlawanan. Sifat-sifat ini membuat pencerminan menjadi salah satu jenis transformasi geometri yang paling mudah dipahami dan digunakan dalam berbagai aplikasi, mulai dari seni hingga teknologi modern.
Dalam artikel ini, kita akan membahas pengertian pencerminan secara lengkap, termasuk jenis-jenisnya, sifat-sifatnya, serta contoh penerapan dalam kehidupan sehari-hari. Selain itu, kita juga akan menjelaskan rumus-rumus yang digunakan untuk menghitung pencerminan terhadap berbagai sumbu dan garis. Dengan demikian, pembaca akan mendapatkan pemahaman yang lebih mendalam tentang konsep pencerminan dan bagaimana penerapannya dalam berbagai situasi.
Pengertian Pencerminan dalam Matematika
Pencerminan, atau yang dikenal juga sebagai refleksi, merupakan salah satu jenis transformasi geometri yang bertujuan untuk memindahkan setiap titik pada suatu objek dengan cara mencerminkannya terhadap sebuah garis atau sumbu tertentu. Dalam konteks matematika, pencerminan tidak hanya berupa bayangan yang terlihat di cermin, tetapi juga melibatkan perubahan koordinat titik-titik tersebut sesuai dengan aturan yang telah ditentukan.
Salah satu ciri utama dari pencerminan adalah bahwa bayangan yang dihasilkan memiliki bentuk dan ukuran yang sama dengan objek aslinya. Namun, posisi bayangan berbeda, karena terletak di sisi yang berlawanan terhadap garis atau sumbu yang digunakan sebagai cermin. Misalnya, jika suatu objek dicerminkan terhadap sumbu-x, maka koordinat y dari setiap titik akan berubah tanda, sedangkan koordinat x tetap sama.
Pencerminan juga memiliki beberapa sifat penting yang harus dipahami. Pertama, jarak antara objek asli dan garis cermin sama dengan jarak antara bayangan dan garis cermin. Kedua, garis yang menghubungkan titik asli dan titik bayangan selalu tegak lurus terhadap garis cermin. Ketiga, pencerminan dapat dilakukan terhadap berbagai jenis garis, seperti sumbu-x, sumbu-y, garis y = x, garis y = -x, atau bahkan garis vertikal dan horizontal lainnya.
Jenis-Jenis Pencerminan dalam Geometri
Dalam geometri, pencerminan dapat dibagi menjadi beberapa jenis berdasarkan garis atau sumbu yang digunakan sebagai cermin. Berikut ini adalah beberapa jenis pencerminan yang umum ditemukan:
1. Pencerminan terhadap Sumbu-X
Pencerminan terhadap sumbu-x adalah transformasi yang memindahkan setiap titik pada objek dengan cara mencerminkannya terhadap sumbu-x. Dalam hal ini, koordinat y dari setiap titik akan berubah tanda, sedangkan koordinat x tetap sama. Secara matematis, jika titik P(x, y) direfleksikan terhadap sumbu-x, maka hasilnya adalah P'(x, -y).
2. Pencerminan terhadap Sumbu-Y
Pencerminan terhadap sumbu-y adalah transformasi yang memindahkan setiap titik pada objek dengan cara mencerminkannya terhadap sumbu-y. Dalam hal ini, koordinat x dari setiap titik akan berubah tanda, sedangkan koordinat y tetap sama. Secara matematis, jika titik P(x, y) direfleksikan terhadap sumbu-y, maka hasilnya adalah P'(-x, y).
3. Pencerminan terhadap Garis y = x
Pencerminan terhadap garis y = x adalah transformasi yang memindahkan setiap titik pada objek dengan cara mencerminkannya terhadap garis y = x. Dalam hal ini, koordinat x dan y dari setiap titik akan saling bertukar. Secara matematis, jika titik P(x, y) direfleksikan terhadap garis y = x, maka hasilnya adalah P'(y, x).
4. Pencerminan terhadap Garis y = -x
Pencerminan terhadap garis y = -x adalah transformasi yang memindahkan setiap titik pada objek dengan cara mencerminkannya terhadap garis y = -x. Dalam hal ini, koordinat x dan y dari setiap titik akan saling bertukar dan berubah tanda. Secara matematis, jika titik P(x, y) direfleksikan terhadap garis y = -x, maka hasilnya adalah P'(-y, -x).
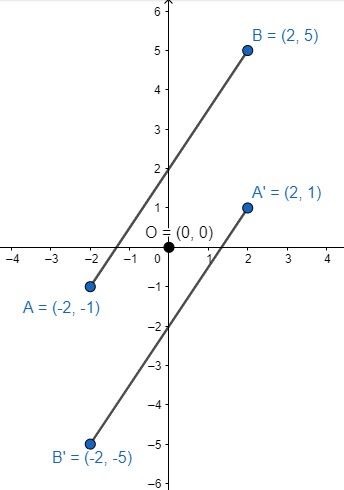
5. Pencerminan terhadap Titik Asal (0, 0)
Pencerminan terhadap titik asal (0, 0) adalah transformasi yang memindahkan setiap titik pada objek dengan cara mencerminkannya terhadap titik asal. Dalam hal ini, koordinat x dan y dari setiap titik akan berubah tanda. Secara matematis, jika titik P(x, y) direfleksikan terhadap titik asal (0, 0), maka hasilnya adalah P'(-x, -y).
6. Pencerminan terhadap Garis Vertikal x = h
Pencerminan terhadap garis vertikal x = h adalah transformasi yang memindahkan setiap titik pada objek dengan cara mencerminkannya terhadap garis x = h. Dalam hal ini, koordinat x dari setiap titik akan dihitung dengan rumus 2h – x, sedangkan koordinat y tetap sama. Secara matematis, jika titik P(x, y) direfleksikan terhadap garis x = h, maka hasilnya adalah P'(2h – x, y).
7. Pencerminan terhadap Garis Horizontal y = k
Pencerminan terhadap garis horizontal y = k adalah transformasi yang memindahkan setiap titik pada objek dengan cara mencerminkannya terhadap garis y = k. Dalam hal ini, koordinat y dari setiap titik akan dihitung dengan rumus 2k – y, sedangkan koordinat x tetap sama. Secara matematis, jika titik P(x, y) direfleksikan terhadap garis y = k, maka hasilnya adalah P'(x, 2k – y).
Contoh Penerapan Pencerminan dalam Kehidupan Sehari-hari
Pencerminan tidak hanya terjadi dalam dunia matematika, tetapi juga sering kita temui dalam kehidupan sehari-hari. Berikut ini adalah beberapa contoh penerapan pencerminan yang umum:
1. Bercermin di Cermin
Salah satu contoh paling sederhana dari pencerminan adalah saat kita bercermin. Ketika kita berdiri di depan cermin, bayangan kita terbentuk di sisi yang berlawanan terhadap cermin. Jarak antara kita dan cermin sama dengan jarak antara bayangan kita dan cermin. Ini adalah contoh pencerminan terhadap garis vertikal (cermin).
2. Genangan Air
Genangan air juga merupakan contoh pencerminan alami. Saat cuaca cerah, genangan air yang jernih dapat mencerminkan bayangan benda-benda di sekitarnya, seperti pohon, bangunan, atau bahkan langit. Fenomena ini terjadi karena permukaan air berperilaku seperti cermin datar.
3. Seni dan Desain Grafis
Dalam seni dan desain grafis, pencerminan sering digunakan untuk menciptakan simetri dan kesimbangan pada karya. Misalnya, dalam desain logo atau gambar ilustrasi, pencerminan dapat digunakan untuk menciptakan efek visual yang menarik dan estetis.
4. Teknologi Augmented Reality (AR)
Teknologi augmented reality (AR) juga memanfaatkan konsep pencerminan untuk menciptakan pengalaman interaktif. Misalnya, dalam aplikasi AR, bayangan objek virtual dapat dicerminkan di layar sesuai dengan posisi dan sudut pandang pengguna.
5. Penerbangan dan Navigasi
Dalam bidang penerbangan dan navigasi, pencerminan digunakan untuk menghitung posisi pesawat atau kapal laut. Dengan memahami prinsip pencerminan, para pilot dan navigator dapat menentukan arah dan posisi mereka secara akurat.
Sifat-Sifat Pencerminan dalam Transformasi Geometri
Pencerminan memiliki beberapa sifat penting yang membedakannya dari jenis transformasi geometri lainnya. Berikut ini adalah beberapa sifat utama dari pencerminan:
1. Simetri Lipat
Pencerminan memiliki sifat simetri lipat, artinya objek yang dicerminkan memiliki bentuk dan ukuran yang sama dengan objek aslinya. Perbedaan hanya terletak pada posisi dan orientasi.
2. Jarak yang Sama
Jarak antara objek asli dan garis cermin sama dengan jarak antara bayangan dan garis cermin. Hal ini menunjukkan bahwa pencerminan bersifat simetris terhadap garis cermin.
3. Garis Hubungan Tegak Lurus
Garis yang menghubungkan titik asli dan titik bayangan selalu tegak lurus terhadap garis cermin. Ini adalah salah satu ciri khas dari pencerminan.
4. Tidak Mengubah Ukuran
Pencerminan tidak mengubah ukuran objek. Bayangan yang dihasilkan memiliki ukuran yang sama dengan objek aslinya, meskipun posisinya berbeda.
5. Tidak Mengubah Bentuk
Bentuk objek yang dicerminkan tetap sama dengan bentuk objek aslinya. Pencerminan hanya mengubah posisi dan orientasi objek, bukan bentuknya.
Rumus-Rumus Pencerminan dalam Matematika
Dalam matematika, pencerminan dapat dihitung menggunakan rumus-rumus yang berbeda tergantung pada jenis garis atau sumbu yang digunakan sebagai cermin. Berikut ini adalah beberapa rumus umum yang digunakan untuk pencerminan:
1. Pencerminan terhadap Sumbu-X
Rumus: $ P(x, y) \rightarrow P'(x, -y) $
2. Pencerminan terhadap Sumbu-Y
Rumus: $ P(x, y) \rightarrow P'(-x, y) $
3. Pencerminan terhadap Garis y = x
Rumus: $ P(x, y) \rightarrow P'(y, x) $
4. Pencerminan terhadap Garis y = -x
Rumus: $ P(x, y) \rightarrow P'(-y, -x) $
5. Pencerminan terhadap Titik Asal (0, 0)
Rumus: $ P(x, y) \rightarrow P'(-x, -y) $
6. Pencerminan terhadap Garis x = h
Rumus: $ P(x, y) \rightarrow P'(2h – x, y) $
7. Pencerminan terhadap Garis y = k
Rumus: $ P(x, y) \rightarrow P'(x, 2k – y) $
Dengan menggunakan rumus-rumus di atas, kita dapat menghitung bayangan dari suatu objek setelah diterapkan pencerminan terhadap berbagai jenis garis atau sumbu. Hal ini sangat berguna dalam berbagai bidang, seperti matematika, seni, dan teknologi.
Contoh Soal Pencerminan dalam Matematika
Untuk memperkuat pemahaman tentang pencerminan, berikut ini adalah beberapa contoh soal yang dapat diselesaikan menggunakan rumus-rumus pencerminan:
Contoh 1:
Tentukan bayangan dari titik A(3, -4) jika dicerminkan terhadap sumbu-x.
Penyelesaian:
Menggunakan rumus pencerminan terhadap sumbu-x:
$ A(3, -4) \rightarrow A'(3, 4) $
Contoh 2:
Tentukan bayangan dari titik B(-2, 5) jika dicerminkan terhadap garis y = x.
Penyelesaian:
Menggunakan rumus pencerminan terhadap garis y = x:
$ B(-2, 5) \rightarrow B'(5, -2) $
Contoh 3:
Tentukan bayangan dari titik C(6, -3) jika dicerminkan terhadap titik asal (0, 0).
Penyelesaian:
Menggunakan rumus pencerminan terhadap titik asal:
$ C(6, -3) \rightarrow C'(-6, 3) $
Contoh 4:
Tentukan bayangan dari garis y = 2x + 1 jika dicerminkan terhadap sumbu-y.
Penyelesaian:
Koordinat x dari setiap titik pada garis akan berubah tanda, sedangkan koordinat y tetap sama. Dengan demikian, persamaan garis setelah pencerminan adalah:
$ y = -2x + 1 $
Kesimpulan
Pencerminan adalah salah satu konsep penting dalam matematika, khususnya dalam bidang geometri. Dengan memahami pencerminan, kita dapat lebih memahami bagaimana objek berubah posisi dan bentuk ketika diterapkan transformasi geometri. Pencerminan memiliki berbagai jenis, termasuk pencerminan terhadap sumbu-x, sumbu-y, garis y = x, garis y = -x, titik asal, garis vertikal, dan garis horizontal. Setiap jenis pencerminan memiliki rumus dan sifat-sifat yang berbeda, tetapi semua memiliki prinsip dasar yang sama, yaitu mencerminkan objek terhadap garis atau sumbu tertentu.
Dalam kehidupan sehari-hari, pencerminan sering kita temui, baik itu dari benda-benda fisik seperti cermin dan genangan air, maupun dalam berbagai bidang seperti seni, desain grafis, dan teknologi. Dengan memahami pencerminan, kita tidak hanya bisa menyelesaikan soal-soal matematika, tetapi juga bisa mengaplikasikan konsep ini dalam berbagai situasi nyata.

















Komentar