Lingkaran adalah bentuk geometris yang sangat umum ditemui dalam kehidupan sehari-hari, baik dalam seni, teknologi, maupun ilmu pengetahuan. Dari roda mobil hingga bintang di langit, lingkaran menjadi bagian dari banyak fenomena alam dan karya manusia. Salah satu unsur penting dalam lingkaran adalah titik pusat lingkaran, yang menjadi dasar dari berbagai konsep matematika terkait lingkaran. Memahami apa itu titik pusat lingkaran dan perannya sangat penting untuk mempelajari geometri, trigonometri, dan bahkan fisika.
Titik pusat lingkaran adalah titik yang berada di tengah-tengah lingkaran, di mana semua titik pada keliling lingkaran memiliki jarak yang sama terhadap titik ini. Jarak tersebut disebut sebagai jari-jari lingkaran. Titik pusat tidak hanya menjadi pusat simetri lingkaran, tetapi juga merupakan acuan utama dalam menghitung luas, keliling, dan berbagai sifat lain dari lingkaran. Tanpa memahami titik pusat, kita tidak akan bisa menentukan ukuran atau posisi lingkaran secara akurat.
Selain itu, titik pusat lingkaran juga menjadi fondasi dalam berbagai aplikasi praktis. Misalnya, dalam desain grafis, pengukuran jarak, atau pemetaan wilayah. Dalam bidang teknik, titik pusat digunakan untuk membuat struktur yang seimbang dan stabil, seperti roda atau piringan. Dengan demikian, memahami titik pusat lingkaran tidak hanya penting dalam matematika, tetapi juga dalam kehidupan nyata.
Apa Itu Titik Pusat Lingkaran?
Secara definisi, titik pusat lingkaran adalah titik yang berada di tengah-tengah lingkaran, sehingga semua titik pada keliling lingkaran memiliki jarak yang sama terhadap titik ini. Titik ini sering dilambangkan dengan huruf O atau P dalam notasi matematika. Dalam geometri, titik pusat menjadi acuan utama untuk menentukan berbagai unsur lain dari lingkaran, seperti jari-jari, diameter, tali busur, dan garis singgung.
Menurut Euclid, seorang matematikawan Yunani kuno, lingkaran adalah himpunan semua titik di bidang datar yang berjarak sama dari suatu titik tetap. Titik tetap ini adalah titik pusat lingkaran. Dengan kata lain, lingkaran adalah bentuk geometris yang simetris sempurna, dan titik pusat menjadi pusat dari kesimetrisan tersebut.
Dalam konteks matematika modern, titik pusat lingkaran sering direpresentasikan dalam sistem koordinat kartesius. Misalnya, jika titik pusat lingkaran berada di titik (h, k), maka persamaan lingkaran dapat ditulis sebagai:
$$
(x – h)^2 + (y – k)^2 = r^2
$$
di mana:
– $x$ dan $y$ adalah koordinat titik pada lingkaran,
– $h$ dan $k$ adalah koordinat titik pusat lingkaran,
– $r$ adalah panjang jari-jari lingkaran.
Dengan menggunakan persamaan ini, kita dapat menentukan posisi titik pusat dan ukuran lingkaran secara tepat.
Peran Titik Pusat Lingkaran dalam Matematika
Titik pusat lingkaran memiliki peran penting dalam berbagai konsep matematika. Berikut beberapa contoh perannya:
-
Menghitung Luas dan Keliling Lingkaran
Luas dan keliling lingkaran bergantung pada jari-jari, yang diukur dari titik pusat ke tepi lingkaran. Rumus luas lingkaran adalah:
$$
L = \pi r^2
$$
sedangkan rumus keliling lingkaran adalah:
$$
K = 2\pi r
$$
Di mana $r$ adalah jari-jari lingkaran, yang diukur dari titik pusat. -
Menentukan Diameter dan Tali Busur
Diameter adalah garis lurus yang melewati titik pusat dan menghubungkan dua titik pada lingkaran. Panjang diameter adalah dua kali jari-jari. Sementara itu, tali busur adalah garis yang menghubungkan dua titik pada lingkaran, tanpa melewati titik pusat. -
Membuat Garis Singgung dan Garis Potong
Garis singgung adalah garis yang menyentuh lingkaran tepat di satu titik. Untuk menentukan garis singgung, kita harus mengetahui posisi titik pusat dan jari-jari lingkaran. Sementara itu, garis potong adalah garis yang memotong lingkaran di dua titik. -
Membentuk Juring dan Tembereng
Juring adalah daerah yang dibatasi oleh dua jari-jari dan sebuah busur. Tembereng adalah daerah yang dibatasi oleh sebuah busur dan tali busur. Kedua bentuk ini juga bergantung pada posisi titik pusat lingkaran. -
Menggambar Lingkaran Secara Akurat
Dalam geometri, untuk menggambar lingkaran secara akurat, kita perlu menentukan titik pusat terlebih dahulu. Titik ini menjadi acuan untuk menarik garis-garis yang membentuk lingkaran.
Bagaimana Menentukan Titik Pusat Lingkaran?
Ada beberapa cara untuk menentukan titik pusat lingkaran, tergantung pada informasi yang tersedia. Berikut beberapa metode umum:
-
Melalui Persamaan Lingkaran
Jika kita memiliki persamaan lingkaran dalam bentuk:
$$
(x – h)^2 + (y – k)^2 = r^2
$$
Maka titik pusat lingkaran adalah $(h, k)$. -
Melalui Garis Sumbu Segitiga
Jika kita memiliki tiga titik yang berada pada lingkaran, kita dapat melukis segitiga sembarang dan kemudian mencari garis sumbu dari dua sisi segitiga. Titik potong dari kedua garis sumbu tersebut adalah titik pusat lingkaran. -
Melalui Garis Bagi Sudut
Jika kita memiliki lingkaran dalam segitiga, kita dapat melukis garis bagi sudut dari dua sudut segitiga. Titik potong dari dua garis bagi tersebut adalah titik pusat lingkaran. -
Melalui Koordinat Titik-Titik pada Lingkaran
Jika kita memiliki beberapa titik yang berada pada lingkaran, kita dapat menghitung titik pusat dengan menggunakan metode statistik atau algoritma komputasi.
Contoh Penerapan Titik Pusat Lingkaran dalam Kehidupan Nyata
Titik pusat lingkaran tidak hanya relevan dalam matematika teoretis, tetapi juga dalam berbagai aplikasi praktis. Berikut beberapa contoh penerapannya:
-
Desain Grafis dan Arsitektur
Dalam desain grafis, titik pusat lingkaran digunakan untuk membuat bentuk-bentuk simetris dan estetis. Dalam arsitektur, titik pusat lingkaran membantu dalam merancang struktur yang seimbang, seperti atap berbentuk lingkaran atau kolam renang bulat. -
Teknik dan Pengukuran
Dalam teknik, titik pusat lingkaran digunakan untuk mengukur jarak, menentukan posisi, dan membuat alat-alat yang berputar, seperti roda atau poros. -
Pemetaan dan Geodesi
Dalam pemetaan, titik pusat lingkaran digunakan untuk menentukan lokasi geografis dan menghitung jarak antar titik. -
Fisika dan Astronomi
Dalam astronomi, orbit planet dan bintang sering dianggap sebagai lingkaran. Titik pusat lingkaran dalam hal ini adalah matahari atau bintang pusat sistem tata surya. -
Kesehatan dan Medis
Dalam medis, titik pusat lingkaran digunakan dalam pencitraan medis, seperti CT scan dan MRI, untuk menentukan posisi organ tubuh.
Kesimpulan
Titik pusat lingkaran adalah salah satu elemen paling penting dalam geometri. Ia menjadi acuan utama dalam menentukan berbagai sifat dan ukuran lingkaran, serta memiliki peran krusial dalam berbagai bidang ilmu dan teknologi. Dengan memahami titik pusat lingkaran, kita tidak hanya dapat menghitung luas dan keliling lingkaran, tetapi juga menerapkannya dalam kehidupan nyata. Oleh karena itu, mempelajari titik pusat lingkaran adalah langkah awal yang penting dalam memahami konsep-konsep matematika yang lebih kompleks.



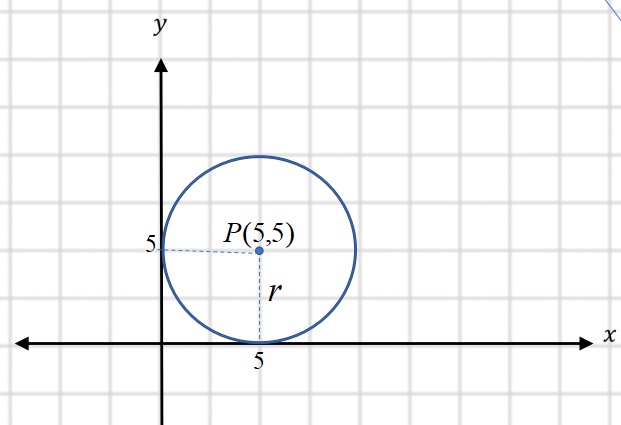
















Komentar