Pengertian dan Rumus Bidang Diagonal Balok dalam Matematika
Balok adalah salah satu bangun ruang tiga dimensi yang sangat umum ditemukan dalam kehidupan sehari-hari. Dari kotak kardus hingga gedung-gedung bertingkat, bentuk balok sering muncul dalam berbagai objek nyata. Dalam matematika, balok memiliki beberapa sifat penting yang perlu dipahami, termasuk bidang diagonal. Bidang diagonal balok merupakan bagian dari struktur balok yang membentuk permukaan datar di dalamnya. Memahami konsep ini tidak hanya membantu dalam memecahkan soal-soal matematika, tetapi juga meningkatkan pemahaman tentang geometri ruang secara keseluruhan.
Bidang diagonal balok adalah permukaan datar yang dibentuk oleh dua diagonal bidang yang saling berhadapan serta dua rusuk yang sejajar. Setiap balok memiliki tiga pasang bidang diagonal, sehingga totalnya ada enam bidang diagonal. Masing-masing bidang diagonal ini memiliki bentuk persegi panjang dan ukuran yang sama dengan pasangannya. Untuk menghitung luas bidang diagonal, kita dapat menggunakan rumus luas persegi panjang, yaitu panjang dikali lebar. Namun, untuk mengetahui panjang diagonal tersebut, kita perlu menggunakan Teorema Pythagoras.
Apa Itu Bidang Diagonal Balok?
Sebelum masuk ke pembahasan rumus, penting untuk memahami konsep dasar dari bidang diagonal balok. Sebuah balok terdiri dari 6 sisi, 12 rusuk, dan 8 titik sudut. Sisi-sisi balok berbentuk persegi atau persegi panjang. Diagonal bidang balok adalah garis lurus yang menghubungkan dua titik sudut yang berlawanan pada satu sisi balok. Sedangkan diagonal ruang adalah garis yang menghubungkan dua titik sudut yang berlawanan di dalam balok, melalui ruang tengah.
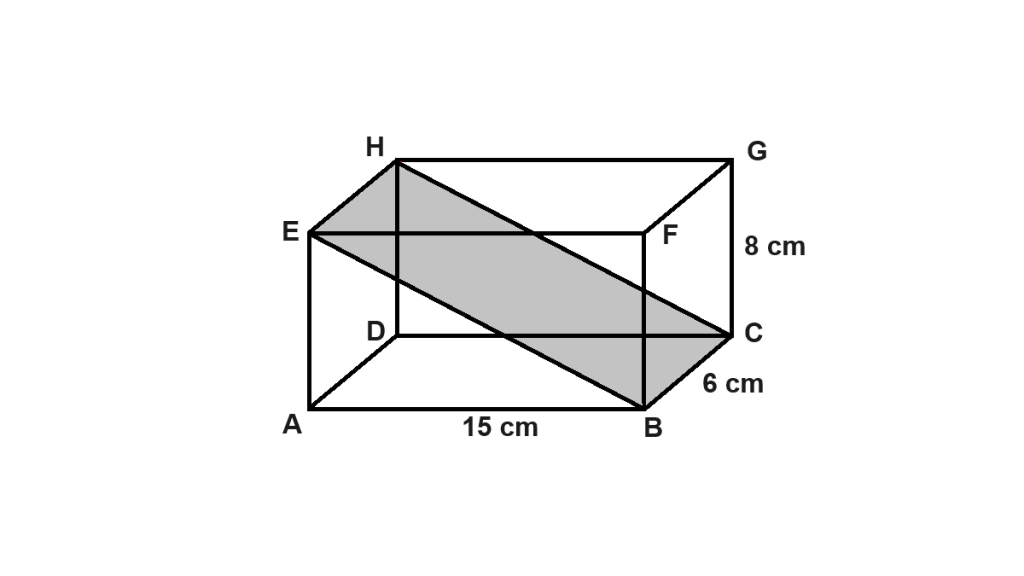
Bidang diagonal balok terbentuk ketika dua diagonal bidang yang sejajar digabungkan bersama dengan dua rusuk yang sejajar. Contohnya, jika kita mengambil dua diagonal bidang pada sisi depan dan belakang balok, maka bidang diagonal akan terbentuk antara kedua sisi tersebut. Bentuk bidang diagonal ini selalu berupa persegi panjang karena sisi balok sendiri berbentuk persegi panjang.
Jenis-Jenis Bidang Diagonal Balok
Dalam sebuah balok, terdapat tiga jenis bidang diagonal, yaitu:
- Bidang Diagonal pada Sisi Depan dan Belakang: Terbentuk oleh dua diagonal bidang pada sisi depan dan belakang balok.
- Bidang Diagonal pada Sisi Kiri dan Kanan: Terbentuk oleh dua diagonal bidang pada sisi kiri dan kanan balok.
- Bidang Diagonal pada Sisi Atas dan Bawah: Terbentuk oleh dua diagonal bidang pada sisi atas dan bawah balok.
Setiap jenis bidang diagonal ini memiliki luas yang sama dengan pasangannya. Misalnya, luas bidang diagonal pada sisi depan sama dengan luas bidang diagonal pada sisi belakang. Hal ini disebabkan oleh sifat simetris dari balok.
Rumus Menghitung Luas Bidang Diagonal Balok
Untuk menghitung luas bidang diagonal balok, kita perlu mengetahui panjang diagonal bidang dan lebar balok. Panjang diagonal bidang dapat dihitung menggunakan Teorema Pythagoras, yaitu:
$$
\text{Diagonal Bidang} = \sqrt{\text{Panjang}^2 + \text{Lebar}^2}
$$
Setelah mengetahui panjang diagonal bidang, kita bisa menghitung luas bidang diagonal dengan rumus:
$$
\text{Luas Bidang Diagonal} = \text{Diagonal Bidang} \times \text{Tinggi}
$$
Contoh:
Jika panjang balok adalah 6 cm, lebar 4 cm, dan tinggi 5 cm, maka:
-
Hitung diagonal bidang pada sisi depan:
$$
\text{Diagonal Bidang} = \sqrt{6^2 + 4^2} = \sqrt{36 + 16} = \sqrt{52} = 2\sqrt{13} \, \text{cm}
$$ -
Hitung luas bidang diagonal:
$$
\text{Luas Bidang Diagonal} = 2\sqrt{13} \times 5 = 10\sqrt{13} \, \text{cm}^2
$$
Dengan demikian, luas bidang diagonal pada sisi depan balok adalah $10\sqrt{13}$ cm².
Fungsi dan Pentingnya Bidang Diagonal Balok
Bidang diagonal balok tidak hanya berguna dalam perhitungan matematika, tetapi juga memiliki aplikasi praktis dalam dunia nyata. Misalnya, dalam desain arsitektur, bidang diagonal digunakan untuk memperkuat struktur bangunan. Dalam teknik sipil, bidang diagonal membantu dalam perhitungan kekuatan material dan distribusi beban.
Selain itu, bidang diagonal juga menjadi bagian penting dalam pengajaran matematika, terutama dalam topik geometri ruang. Siswa diajarkan untuk mengidentifikasi dan menghitung bidang diagonal sebagai bagian dari pembelajaran tentang bangun ruang. Pemahaman tentang bidang diagonal membantu siswa memahami sifat-sifat bangun ruang dan hubungan antar elemen-elemen dalam balok.
Contoh Soal Mengenai Bidang Diagonal Balok
Berikut adalah contoh soal yang berkaitan dengan bidang diagonal balok:
Soal 1:
Sebuah balok memiliki panjang 10 cm, lebar 6 cm, dan tinggi 8 cm. Hitunglah luas salah satu bidang diagonal balok!
Penyelesaian:
Langkah 1: Hitung diagonal bidang pada sisi depan:
$$
\text{Diagonal Bidang} = \sqrt{10^2 + 6^2} = \sqrt{100 + 36} = \sqrt{136} = 2\sqrt{34} \, \text{cm}
$$
Langkah 2: Hitung luas bidang diagonal:
$$
\text{Luas Bidang Diagonal} = 2\sqrt{34} \times 8 = 16\sqrt{34} \, \text{cm}^2
$$
Soal 2:
Sebuah balok memiliki luas bidang diagonal sebesar 120 cm². Jika tinggi balok adalah 10 cm, hitunglah panjang diagonal bidang balok!
Penyelesaian:
Kita tahu bahwa:
$$
\text{Luas Bidang Diagonal} = \text{Diagonal Bidang} \times \text{Tinggi}
$$
Maka:
$$
120 = \text{Diagonal Bidang} \times 10 \
\text{Diagonal Bidang} = \frac{120}{10} = 12 \, \text{cm}
$$
Dengan demikian, panjang diagonal bidang balok adalah 12 cm.
Manfaat Memahami Bidang Diagonal Balok
Memahami bidang diagonal balok memberikan banyak manfaat, baik dalam studi matematika maupun dalam penerapan nyata. Berikut beberapa manfaat utamanya:
- Meningkatkan Kemampuan Analitis: Memahami bidang diagonal membantu siswa dalam mengembangkan kemampuan analitis dan logika.
- Mudah dalam Perhitungan Geometri: Pemahaman tentang bidang diagonal mempermudah dalam perhitungan luas permukaan dan volume balok.
- Aplikasi Praktis: Bidang diagonal digunakan dalam desain bangunan, teknik sipil, dan seni grafis.
- Membantu dalam Ujian Nasional: Soal-soal tentang balok sering muncul dalam ujian nasional, terutama dalam materi dimensi tiga.
Kesimpulan
Bidang diagonal balok adalah bagian penting dari struktur balok yang memiliki fungsi dan kegunaan yang luas. Dengan memahami konsep dan rumusnya, kita tidak hanya dapat menyelesaikan soal-soal matematika, tetapi juga meningkatkan pemahaman tentang geometri ruang. Dalam kehidupan sehari-hari, bidang diagonal juga memiliki peran penting dalam berbagai bidang, seperti arsitektur dan teknik. Oleh karena itu, mempelajari bidang diagonal balok adalah langkah penting dalam memperkaya pengetahuan matematika dan mempersiapkan diri untuk berbagai tantangan di masa depan.
Dengan memahami konsep dan rumus bidang diagonal balok, kita dapat lebih mudah menghadapi soal-soal matematika yang berkaitan dengan bangun ruang. Selain itu, pemahaman ini juga membantu dalam merancang dan membangun berbagai struktur yang membutuhkan kekuatan dan stabilitas. Dengan begitu, bidang diagonal balok bukan hanya sekadar konsep teoritis, tetapi juga memiliki nilai praktis yang signifikan.


















Komentar