Dalam dunia matematika, konsep persamaan dan pertidaksamaan linear satu variabel menjadi fondasi penting yang sering muncul dalam berbagai bidang studi. Baik itu di tingkat sekolah menengah atau universitas, pemahaman tentang materi ini sangat krusial untuk mengembangkan kemampuan analitis dan logika. Persamaan linear satu variabel (PLSV) dan pertidaksamaan linear satu variabel (PtLSV) adalah dua konsep yang saling berkaitan namun memiliki perbedaan mendasar dalam penggunaan dan penyelesaian.
Persamaan linear satu variabel adalah kalimat matematika yang menyatakan kesamaan antara dua ekspresi, salah satunya mengandung variabel tunggal. Sementara itu, pertidaksamaan linear satu variabel menyatakan hubungan ketidaksamaan antara dua ekspresi. Kedua konsep ini tidak hanya digunakan dalam pelajaran matematika, tetapi juga memiliki aplikasi nyata dalam kehidupan sehari-hari, seperti dalam perencanaan keuangan, optimasi produksi, dan analisis data.
Pemahaman yang baik tentang persamaan dan pertidaksamaan linear satu variabel membantu seseorang dalam menyelesaikan masalah yang melibatkan batasan nilai atau hubungan antar variabel. Dengan mempelajari cara menyelesaikan soal-soal terkait, siswa dan pembaca dapat meningkatkan kemampuan mereka dalam berpikir kritis dan menyelesaikan masalah secara efisien.
Selain itu, pemahaman akan sifat-sifat dasar dari persamaan dan pertidaksamaan linear satu variabel juga penting karena memberikan landasan untuk mempelajari topik-topik matematika yang lebih kompleks. Dengan demikian, artikel ini akan membahas secara mendalam tentang persamaan dan pertidaksamaan linear satu variabel, mulai dari definisi hingga contoh soal dan penerapannya dalam kehidupan nyata.
Pengertian Persamaan Linear Satu Variabel
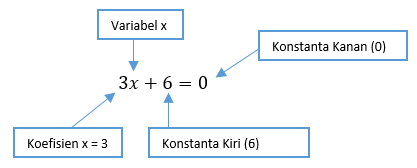
Persamaan linear satu variabel (PLSV) adalah bentuk persamaan matematika yang hanya memiliki satu variabel dan pangkat tertinggi dari variabel tersebut adalah satu. Dalam bentuk umum, PLSV dapat ditulis sebagai:
$$ ax + b = 0 $$
di mana:
– $ a $ adalah koefisien dari variabel $ x $,
– $ b $ adalah konstanta,
– $ x $ adalah variabel yang nilainya belum diketahui.
Contoh dari PLSV adalah $ 2x + 3 = 7 $. Untuk menyelesaikan persamaan ini, kita perlu mencari nilai $ x $ yang memenuhi persamaan tersebut. Proses penyelesaiannya melibatkan manipulasi aljabar, seperti mengisolasi variabel pada satu sisi persamaan.
Sifat-sifat utama dari PLSV meliputi:
1. Penjumlahan dan Pengurangan: Jika kedua ruas persamaan ditambah atau dikurangi dengan bilangan yang sama, maka hasilnya tetap benar.
2. Perkalian dan Pembagian: Jika kedua ruas persamaan dikali atau dibagi dengan bilangan yang sama (selama bilangan tersebut bukan nol), maka hasilnya tetap benar.
3. Hukum Komutatif dan Asosiatif: Hukum ini berlaku dalam operasi penjumlahan dan perkalian.
Dengan memahami sifat-sifat ini, siswa dapat lebih mudah menyelesaikan berbagai jenis soal PLSV. Selain itu, pemahaman tentang konsep-konsep dasar seperti variabel, koefisien, dan konstanta juga sangat penting. Misalnya, variabel adalah simbol yang digunakan untuk mewakili bilangan yang belum diketahui, sedangkan koefisien adalah bilangan yang mengalikan variabel.
Pengertian Pertidaksamaan Linear Satu Variabel
Pertidaksamaan linear satu variabel (PtLSV) adalah kalimat matematika yang menyatakan hubungan ketidaksamaan antara dua ekspresi, salah satunya mengandung variabel tunggal. PtLSV menggunakan tanda-tanda seperti <, >, ≤, atau ≥ untuk menunjukkan hubungan antara dua ekspresi. Bentuk umum dari PtLSV adalah:
$$ ax + b < 0 \quad \text{atau} \quad ax + b > 0 $$
di mana:
– $ a $ adalah koefisien dari variabel $ x $,
– $ b $ adalah konstanta,
– $ x $ adalah variabel yang nilainya belum diketahui.
Contoh dari PtLSV adalah $ 2x + 3 > 7 $. Untuk menyelesaikan pertidaksamaan ini, kita perlu mencari semua nilai $ x $ yang memenuhi pertidaksamaan tersebut. Proses penyelesaiannya mirip dengan PLSV, tetapi dengan tambahan aturan khusus, yaitu jika kedua ruas dikali atau dibagi dengan bilangan negatif, tanda pertidaksamaan harus dibalik.
Beberapa sifat penting dari PtLSV meliputi:
1. Penjumlahan dan Pengurangan: Jika kedua ruas pertidaksamaan ditambah atau dikurangi dengan bilangan yang sama, maka hasilnya tetap benar.
2. Perkalian dan Pembagian: Jika kedua ruas dikali atau dibagi dengan bilangan positif, tanda pertidaksamaan tetap. Namun, jika dikali atau dibagi dengan bilangan negatif, tanda pertidaksamaan harus dibalik.
3. Ketidaksamaan Rantai: Dalam beberapa kasus, PtLSV dapat dinyatakan dalam bentuk rantai, seperti $ a < x < b $, yang berarti $ x $ berada dalam rentang antara $ a $ dan $ b $.
Pemahaman tentang PtLSV sangat penting karena banyak digunakan dalam berbagai situasi nyata. Misalnya, dalam perencanaan keuangan, PtLSV dapat digunakan untuk menentukan batasan pengeluaran agar tidak melebihi anggaran. Dalam optimasi produksi, PtLSV membantu menentukan jumlah minimum produk yang harus diproduksi untuk mencapai target keuntungan tertentu.
Perbedaan Antara Persamaan dan Pertidaksamaan Linear Satu Variabel
Meskipun persamaan dan pertidaksamaan linear satu variabel (PLSV dan PtLSV) memiliki kesamaan dalam struktur dan tujuan, terdapat perbedaan mendasar antara keduanya. PLSV bertujuan untuk menemukan nilai tunggal dari variabel yang memenuhi persamaan, sedangkan PtLSV mencari himpunan nilai yang memenuhi pertidaksamaan.
Secara teknis, PLSV menggunakan tanda sama dengan (=), sedangkan PtLSV menggunakan tanda pertidaksamaan (<, >, ≤, atau ≥). Contohnya, jika kita memiliki persamaan $ 2x + 3 = 7 $, solusinya adalah $ x = 2 $. Namun, jika kita memiliki pertidaksamaan $ 2x + 3 > 7 $, solusinya adalah $ x > 2 $, yang berarti semua bilangan real yang lebih besar dari 2.
Salah satu hal yang perlu diperhatikan saat menyelesaikan PtLSV adalah aturan pembalikan tanda ketika mengalikan atau membagi dengan bilangan negatif. Misalnya, jika kita memiliki pertidaksamaan $ -2x > 4 $, dan kita membagi kedua ruas dengan -2, tanda pertidaksamaan harus dibalik, sehingga menjadi $ x < -2 $.
Selain itu, PLSV biasanya memiliki solusi tunggal, sementara PtLSV bisa memiliki solusi dalam bentuk interval atau himpunan tak hingga. Hal ini membuat PtLSV lebih fleksibel dalam menggambarkan situasi nyata yang melibatkan batasan nilai.
Pemahaman tentang perbedaan ini sangat penting bagi siswa dan pembaca, karena membantu mereka dalam memilih metode penyelesaian yang tepat sesuai dengan jenis soal yang diberikan. Selain itu, pemahaman ini juga membuka jalan untuk mempelajari konsep-konsep matematika yang lebih lanjut, seperti sistem persamaan linear dan pertidaksamaan kuadrat.
Contoh Soal dan Penyelesaian Persamaan Linear Satu Variabel
Untuk memperdalam pemahaman tentang persamaan linear satu variabel (PLSV), berikut ini beberapa contoh soal beserta penyelesaiannya:
Contoh Soal 1
Selesaikan persamaan $ 3x + 4 = 10 $.
Penyelesaian:
Langkah 1: Kurangi kedua ruas dengan 4.
$$ 3x + 4 – 4 = 10 – 4 $$
$$ 3x = 6 $$
Langkah 2: Bagi kedua ruas dengan 3.
$$ \frac{3x}{3} = \frac{6}{3} $$
$$ x = 2 $$
Jadi, solusi dari persamaan tersebut adalah $ x = 2 $.
Contoh Soal 2
Selesaikan persamaan $ 5x – 7 = 8 $.
Penyelesaian:
Langkah 1: Tambahkan 7 ke kedua ruas.
$$ 5x – 7 + 7 = 8 + 7 $$
$$ 5x = 15 $$
Langkah 2: Bagi kedua ruas dengan 5.
$$ \frac{5x}{5} = \frac{15}{5} $$
$$ x = 3 $$
Solusi dari persamaan ini adalah $ x = 3 $.
Contoh Soal 3
Selesaikan persamaan $ 2(x + 3) = 14 $.
Penyelesaian:
Langkah 1: Gunakan distribusi untuk menguraikan ruas kiri.
$$ 2x + 6 = 14 $$
Langkah 2: Kurangi kedua ruas dengan 6.
$$ 2x + 6 – 6 = 14 – 6 $$
$$ 2x = 8 $$
Langkah 3: Bagi kedua ruas dengan 2.
$$ \frac{2x}{2} = \frac{8}{2} $$
$$ x = 4 $$
Solusi dari persamaan ini adalah $ x = 4 $.
Dengan menyelesaikan contoh soal-soal di atas, siswa dapat memahami langkah-langkah dasar dalam menyelesaikan PLSV. Selain itu, latihan ini juga membantu meningkatkan kemampuan mereka dalam melakukan manipulasi aljabar dan menyelesaikan masalah secara sistematis.
Contoh Soal dan Penyelesaian Pertidaksamaan Linear Satu Variabel
Untuk memperdalam pemahaman tentang pertidaksamaan linear satu variabel (PtLSV), berikut ini beberapa contoh soal beserta penyelesaiannya:
Contoh Soal 1
Selesaikan pertidaksamaan $ 3x + 4 > 10 $.
Penyelesaian:
Langkah 1: Kurangi kedua ruas dengan 4.
$$ 3x + 4 – 4 > 10 – 4 $$
$$ 3x > 6 $$
Langkah 2: Bagi kedua ruas dengan 3.
$$ \frac{3x}{3} > \frac{6}{3} $$
$$ x > 2 $$
Jadi, solusi dari pertidaksamaan ini adalah $ x > 2 $.
Contoh Soal 2
Selesaikan pertidaksamaan $ 5x – 7 < 8 $.
Penyelesaian:
Langkah 1: Tambahkan 7 ke kedua ruas.
$$ 5x – 7 + 7 < 8 + 7 $$
$$ 5x < 15 $$
Langkah 2: Bagi kedua ruas dengan 5.
$$ \frac{5x}{5} < \frac{15}{5} $$
$$ x < 3 $$
Solusi dari pertidaksamaan ini adalah $ x < 3 $.
Contoh Soal 3
Selesaikan pertidaksamaan $ 2(x + 3) \geq 14 $.
Penyelesaian:
Langkah 1: Gunakan distribusi untuk menguraikan ruas kiri.
$$ 2x + 6 \geq 14 $$
Langkah 2: Kurangi kedua ruas dengan 6.
$$ 2x + 6 – 6 \geq 14 – 6 $$
$$ 2x \geq 8 $$
Langkah 3: Bagi kedua ruas dengan 2.
$$ \frac{2x}{2} \geq \frac{8}{2} $$
$$ x \geq 4 $$
Solusi dari pertidaksamaan ini adalah $ x \geq 4 $.
Dengan menyelesaikan contoh soal-soal di atas, siswa dapat memahami langkah-langkah dasar dalam menyelesaikan PtLSV. Selain itu, latihan ini juga membantu meningkatkan kemampuan mereka dalam melakukan manipulasi aljabar dan menyelesaikan masalah secara sistematis.
Aplikasi Praktis Persamaan dan Pertidaksamaan Linear Satu Variabel
Persamaan dan pertidaksamaan linear satu variabel (PLSV dan PtLSV) tidak hanya digunakan dalam pelajaran matematika, tetapi juga memiliki berbagai aplikasi praktis dalam kehidupan sehari-hari. Berikut ini beberapa contoh penerapan PLSV dan PtLSV dalam situasi nyata:
-
Perencanaan Keuangan
Dalam perencanaan anggaran, PLSV dan PtLSV digunakan untuk menentukan batasan pengeluaran agar tidak melebihi pendapatan. Misalnya, jika seseorang memiliki pendapatan bulanan sebesar Rp5.000.000 dan ingin menyisihkan minimal Rp1.000.000 untuk tabungan, maka pertidaksamaan $ x \leq 4.000.000 $ dapat digunakan untuk memastikan bahwa pengeluaran tidak melebihi batas yang ditentukan. -
Optimasi Produksi
Dalam bisnis, PLSV dan PtLSV digunakan untuk menentukan jumlah minimum produk yang harus diproduksi agar mencapai target keuntungan tertentu. Misalnya, jika biaya produksi per unit adalah Rp10.000 dan harga jual per unit adalah Rp15.000, maka persamaan $ 15x – 10x = 5x $ dapat digunakan untuk menentukan jumlah produk yang harus dijual agar mendapatkan keuntungan sebesar Rp100.000. -
Analisis Data
Dalam analisis statistik, PLSV dan PtLSV digunakan untuk menentukan rentang nilai yang signifikan secara statistik. Misalnya, jika rata-rata nilai ujian adalah 70 dan deviasi standar adalah 10, maka pertidaksamaan $ 60 \leq x \leq 80 $ dapat digunakan untuk menentukan rentang nilai yang dianggap normal. -
Perhitungan Biaya Transportasi
Dalam perhitungan biaya transportasi, PLSV dan PtLSV digunakan untuk menentukan biaya terendah yang dapat dicapai. Misalnya, jika biaya sewa mobil adalah Rp200.000 per hari dan biaya bensin per kilometer adalah Rp5.000, maka persamaan $ 200.000 + 5.000x $ dapat digunakan untuk menentukan total biaya perjalanan berdasarkan jarak tempuh.
Dengan memahami penerapan PLSV dan PtLSV dalam kehidupan sehari-hari, siswa dan pembaca dapat melihat bagaimana konsep matematika ini relevan dengan situasi nyata. Hal ini juga membantu meningkatkan motivasi belajar dan memperkuat pemahaman tentang pentingnya matematika dalam kehidupan sehari-hari.

















Komentar