Pahami Rumus Fungsi Invers dengan Mudah dan Lengkap

Matematika sering dianggap sebagai pelajaran yang menantang, terutama ketika mempelajari konsep-konsep seperti fungsi invers. Namun, jika dipahami dengan benar, rumus fungsi invers bisa menjadi alat yang sangat berguna dalam menyelesaikan berbagai masalah matematika. Fungsi invers adalah kebalikan dari fungsi asalnya, sehingga membantu kita mengubah arah hubungan antara variabel-variabel dalam suatu persamaan. Dengan memahami cara mencari invers fungsi, siswa akan lebih mudah menghadapi soal-soal kompleks yang melibatkan fungsi komposisi atau persamaan yang tidak langsung.

Fungsi invers memiliki peran penting dalam berbagai bidang, mulai dari ilmu pengetahuan hingga teknologi. Di sekolah, materi ini sering muncul dalam ujian akhir semester atau ujian nasional, sehingga pemahaman yang mendalam sangat diperlukan. Meski begitu, banyak siswa merasa kesulitan karena terlalu fokus pada penghafalan rumus tanpa memahami konsep dasarnya. Oleh karena itu, artikel ini akan membahas secara lengkap tentang rumus fungsi invers, cara mencari invers fungsi, serta contoh soal yang dapat digunakan untuk latihan.

Pemahaman tentang fungsi invers juga sangat bermanfaat dalam studi lanjut, seperti kalkulus, statistik, dan analisis data. Selain itu, kemampuan dalam menentukan fungsi invers bisa meningkatkan keterampilan logika dan pemecahan masalah. Untuk itu, mari kita pelajari bersama bagaimana cara kerja fungsi invers dan bagaimana menggunakannya dalam berbagai situasi.

Apa Itu Fungsi Invers?

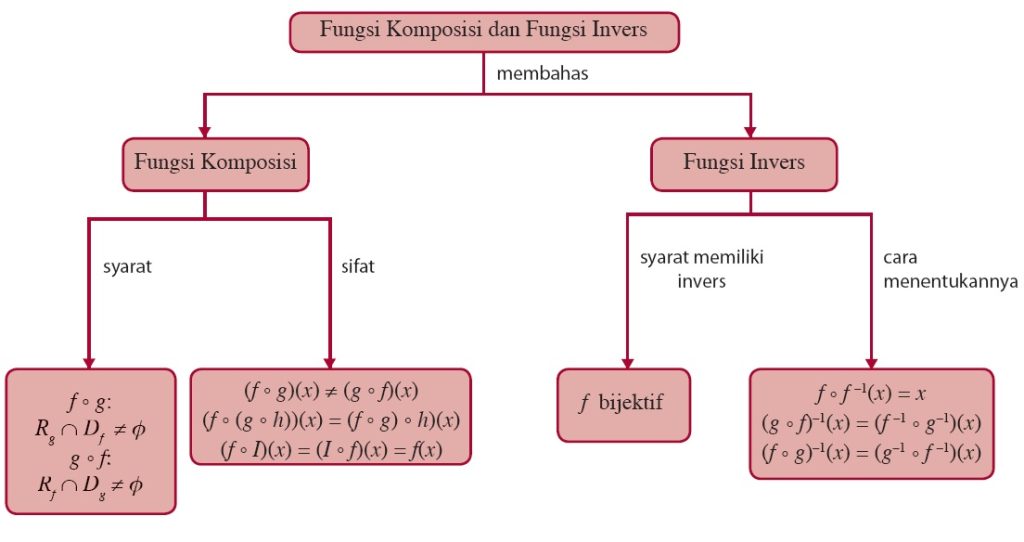
Fungsi invers adalah kebalikan dari fungsi asli. Jika sebuah fungsi f(x) memetakan elemen dari domain ke kodomain, maka fungsi invers f⁻¹(x) akan memetakan elemen dari kodomain kembali ke domain. Dengan kata lain, fungsi invers membalikkan proses yang dilakukan oleh fungsi asli. Contohnya, jika f(x) = 2x + 3, maka fungsi inversnya adalah f⁻¹(x) = (x – 3)/2.

Namun, tidak semua fungsi memiliki invers. Syarat agar suatu fungsi memiliki invers adalah bahwa fungsi tersebut harus bijektif, artinya fungsi tersebut harus satu-satu (injektif) dan onto (surjektif). Dengan kata lain, setiap elemen di domain harus dipetakan ke satu elemen di kodomain, dan setiap elemen di kodomain harus memiliki pasangan di domain.

Untuk memahami lebih jelas, bayangkan fungsi sebagai mesin yang menerima input (domain) dan menghasilkan output (kodomain). Fungsi invers adalah mesin yang menerima output dari fungsi asli dan menghasilkan kembali input aslinya. Jadi, jika f(x) = y, maka f⁻¹(y) = x.

Cara Mencari Fungsi Invers

Mencari fungsi invers tidak terlalu sulit jika Anda mengikuti langkah-langkah yang tepat. Berikut adalah tiga tahapan utama untuk menentukan fungsi invers:

1. Ubah bentuk y = f(x) ke dalam bentuk x = f(y)
   
   Langkah pertama adalah mengganti f(x) dengan y, lalu menyelesaikan persamaan untuk x dalam bentuk y.

2. Tulis x sebagai f⁻¹(y)
   
   Setelah x ditemukan dalam bentuk y, ganti x dengan f⁻¹(y), sehingga diperoleh f⁻¹(y) = x.

3. Ubah variabel y dengan x
   
   Terakhir, ubah variabel y menjadi x agar hasilnya berbentuk fungsi invers biasanya ditulis sebagai f⁻¹(x).

   Read also: rumus fraksi mol dan cara menghitungnya dalam kimia

Contoh sederhana:

Jika f(x) = 2x + 3, maka:
– Ganti f(x) dengan y: y = 2x + 3
– Selesaikan untuk x: x = (y – 3)/2
– Ganti x dengan f⁻¹(y): f⁻¹(y) = (y – 3)/2
– Ubah y menjadi x: f⁻¹(x) = (x – 3)/2

Dengan demikian, fungsi invers dari f(x) = 2x + 3 adalah f⁻¹(x) = (x – 3)/2.

Rumus Fungsi Invers untuk Berbagai Jenis Fungsi

Berikut adalah beberapa rumus fungsi invers untuk berbagai jenis fungsi umum:

1. Fungsi Linear

• Fungsi Asli: f(x) = ax + b
• Fungsi Invers: f⁻¹(x) = (x – b)/a

2. Fungsi Rasional

• Fungsi Asli: f(x) = (ax + b)/(cx + d)
• Fungsi Invers: f⁻¹(x) = (bx – a)/(cx – d)

3. Fungsi Kuadrat

• Fungsi Asli: f(x) = ax² + bx + c
• Fungsi Invers: f⁻¹(x) = √[(x – c)/a] – b/(2a)

4. Fungsi Logaritma

• Fungsi Asli: f(x) = log_a(x)
• Fungsi Invers: f⁻¹(x) = a^x

5. Fungsi Eksponensial

• Fungsi Asli: f(x) = a^x
• Fungsi Invers: f⁻¹(x) = log_a(x)

Selain itu, ada juga rumus khusus untuk fungsi komposisi dan invers. Misalnya:
– (f o g)⁻¹(x) = g⁻¹(f⁻¹(x))

– (f o g o h)⁻¹(x) = h⁻¹(g⁻¹(f⁻¹(x)))

Contoh Soal Fungsi Invers

Berikut adalah beberapa contoh soal fungsi invers beserta penyelesaiannya:

Contoh 1

Soal: Tentukan fungsi invers dari f(x) = 3x + 6.

Penyelesaian:

1. Ganti f(x) dengan y: y = 3x + 6

2. Selesaikan untuk x: x = (y – 6)/3

3. Ganti x dengan f⁻¹(y): f⁻¹(y) = (y – 6)/3

4. Ubah y menjadi x: f⁻¹(x) = (x – 6)/3

Contoh 2

Soal: Tentukan fungsi invers dari f(x) = (2x + 1)/(x – 3).

Penyelesaian:

1. Ganti f(x) dengan y: y = (2x + 1)/(x – 3)

2. Selesaikan untuk x:

– Kalikan kedua sisi dengan (x – 3): y(x – 3) = 2x + 1

– Hitung: xy – 3y = 2x + 1

– Pindahkan x ke satu sisi: xy – 2x = 3y + 1

– Faktorkan x: x(y – 2) = 3y + 1

– Selesaikan: x = (3y + 1)/(y – 2)

3. Ganti x dengan f⁻¹(y): f⁻¹(y) = (3y + 1)/(y – 2)

4. Ubah y menjadi x: f⁻¹(x) = (3x + 1)/(x – 2)

Tips untuk Memahami Fungsi Invers

1. Pahami Konsep Dasar
   
   Jangan hanya menghafal rumus, tetapi pahami bagaimana fungsi bekerja dan bagaimana inversnya membalikkan proses tersebut.

2. Latihan Banyak Soal
   
   Latihan soal akan membantu Anda mengingat dan memahami cara menerapkan rumus fungsi invers dalam berbagai situasi.

3. Gunakan Grafik
   
   Menggambar grafik fungsi dan grafik inversnya dapat membantu Anda memvisualisasikan hubungan antara keduanya.

4. Konsultasi dengan Tutor
   
   Jika masih merasa bingung, Anda bisa belajar dengan tutor privat yang ahli dalam matematika. Mereka akan membantu Anda memahami konsep-konsep yang sulit dengan cara yang lebih mudah.

Penutup

Fungsi invers adalah salah satu konsep penting dalam matematika yang memiliki banyak aplikasi dalam kehidupan sehari-hari. Dengan memahami rumus fungsi invers dan cara mencarinya, Anda akan lebih mudah menyelesaikan berbagai masalah matematika yang melibatkan fungsi. Selain itu, pemahaman tentang fungsi invers juga akan memperkuat dasar Anda dalam mempelajari topik-topik matematika lanjutan seperti kalkulus, statistik, dan analisis data.

Jika Anda merasa masih kesulitan, jangan ragu untuk mencari bantuan dari guru atau tutor privat. Dengan latihan yang cukup dan pemahaman yang mendalam, Anda pasti akan mampu menguasai konsep ini. Semoga artikel ini membantu Anda dalam memahami rumus fungsi invers dengan lebih mudah dan menyenangkan.