Pengertian bilangan rasional adalah salah satu konsep dasar dalam matematika yang sering muncul dalam berbagai topik seperti pecahan, desimal, dan persamaan. Dalam dunia pendidikan, pemahaman tentang bilangan rasional sangat penting karena menjadi fondasi untuk memahami operasi matematika yang lebih kompleks. Bilangan rasional tidak hanya digunakan dalam konteks teoritis, tetapi juga dalam kehidupan sehari-hari, seperti perhitungan keuangan, pengukuran, dan analisis data.
Bilangan rasional dapat dinyatakan sebagai hasil bagi dua bilangan bulat, dengan syarat penyebutnya tidak nol. Artinya, setiap bilangan yang bisa ditulis dalam bentuk $ \frac{a}{b} $, di mana $ a $ dan $ b $ adalah bilangan bulat dan $ b \neq 0 $, termasuk bilangan rasional. Contoh sederhana dari bilangan rasional adalah 1/2, 3/4, atau bahkan bilangan bulat seperti 5, yang dapat ditulis sebagai 5/1. Pemahaman ini membantu kita mengenali bahwa bilangan rasional mencakup berbagai jenis angka, baik itu bilangan bulat, pecahan, maupun desimal berhenti atau berulang.
Selain itu, pengertian bilangan rasional juga memperluas wawasan kita tentang bagaimana bilangan-bilangan ini memiliki sifat-sifat khusus. Misalnya, bilangan rasional tertutup terhadap operasi penjumlahan dan perkalian, artinya jika kita menjumlahkan atau mengalikan dua bilangan rasional, hasilnya akan tetap merupakan bilangan rasional. Sifat-sifat lain seperti komutatif, asosiatif, dan distributif juga berlaku pada bilangan rasional, memberikan struktur yang konsisten dalam perhitungan matematika.
Dengan memahami pengertian bilangan rasional, kita tidak hanya menambah pengetahuan matematika, tetapi juga meningkatkan kemampuan logika dan analisis dalam memecahkan masalah. Artikel ini akan membahas secara rinci pengertian bilangan rasional, contohnya, serta sifat-sifatnya, agar pembaca dapat memahami konsep ini dengan lebih jelas dan mendalam.
Pengertian Bilangan Rasional
Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk pecahan $ \frac{a}{b} $, di mana $ a $ dan $ b $ adalah bilangan bulat, serta $ b \neq 0 $. Konsep ini berasal dari kata “rasio” dalam bahasa Inggris, yang menggambarkan hubungan antara dua bilangan. Oleh karena itu, bilangan rasional sering disebut sebagai bilangan yang dapat dinyatakan dalam bentuk perbandingan atau rasio.
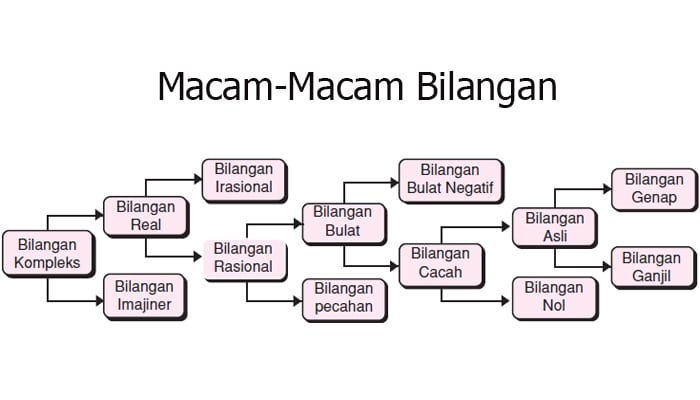
Secara umum, bilangan rasional mencakup berbagai jenis angka, termasuk bilangan bulat, pecahan, dan desimal berhenti atau berulang. Contoh bilangan rasional meliputi:
- Bilangan bulat: Seperti 1, 2, -3, 0, dan 5. Bilangan-bilangan ini dapat dinyatakan sebagai pecahan dengan penyebut 1, misalnya 5 = 5/1.
- Pecahan: Seperti $ \frac{1}{2} $, $ \frac{3}{4} $, dan $ \frac{-5}{6} $.
- Desimal berhenti: Seperti 0,5 (yang sama dengan $ \frac{1}{2} $) dan 1,25 (yang sama dengan $ \frac{5}{4} $).
- Desimal berulang: Seperti 0,333… (yang sama dengan $ \frac{1}{3} $) dan 2,555… (yang sama dengan $ \frac{23}{9} $).
Bilangan rasional berbeda dengan bilangan irasional, yang tidak dapat dinyatakan dalam bentuk pecahan dua bilangan bulat. Contoh bilangan irasional adalah $ \sqrt{2} $, $ \pi $, dan $ e $, yang memiliki desimal tak berujung dan tidak berulang.
Sifat-Sifat Bilangan Rasional
Bilangan rasional memiliki beberapa sifat khusus yang membuatnya mudah dikelola dalam operasi matematika. Berikut adalah sifat-sifat utama dari bilangan rasional:
- Tertutup terhadap operasi penjumlahan dan perkalian
Jika kita menjumlahkan atau mengalikan dua bilangan rasional, hasilnya selalu merupakan bilangan rasional. Misalnya: - $ \frac{1}{2} + \frac{1}{3} = \frac{5}{6} $
-
$ \frac{2}{3} \times \frac{3}{4} = \frac{6}{12} = \frac{1}{2} $
-
Sifat Komutatif
Operasi penjumlahan dan perkalian pada bilangan rasional bersifat komutatif, artinya urutan bilangan tidak memengaruhi hasil. Contoh: - $ \frac{1}{2} + \frac{1}{3} = \frac{1}{3} + \frac{1}{2} $
-
$ \frac{2}{3} \times \frac{3}{4} = \frac{3}{4} \times \frac{2}{3} $
-
Sifat Asosiatif
Sifat asosiatif berlaku pada penjumlahan dan perkalian, artinya pengelompokan bilangan tidak memengaruhi hasil. Contoh: - $ (\frac{1}{2} + \frac{1}{3}) + \frac{1}{6} = \frac{1}{2} + (\frac{1}{3} + \frac{1}{6}) $
-
$ (\frac{2}{3} \times \frac{3}{4}) \times \frac{4}{5} = \frac{2}{3} \times (\frac{3}{4} \times \frac{4}{5}) $
-
Sifat Distributif
Sifat distributif menyatakan bahwa perkalian dapat didistribusikan terhadap penjumlahan. Contoh: -
$ \frac{2}{3} \times (\frac{1}{2} + \frac{1}{3}) = (\frac{2}{3} \times \frac{1}{2}) + (\frac{2}{3} \times \frac{1}{3}) $
-
Elemen Identitas
Setiap bilangan rasional memiliki elemen identitas untuk penjumlahan dan perkalian: - Elemen identitas penjumlahan adalah 0, karena $ x + 0 = x $.
-
Elemen identitas perkalian adalah 1, karena $ x \times 1 = x $.
-
Invers Penjumlahan dan Perkalian
Setiap bilangan rasional memiliki invers penjumlahan dan perkalian, kecuali nol. Contoh: - Invers penjumlahan dari $ \frac{1}{2} $ adalah $ -\frac{1}{2} $, karena $ \frac{1}{2} + (-\frac{1}{2}) = 0 $.
-
Invers perkalian dari $ \frac{2}{3} $ adalah $ \frac{3}{2} $, karena $ \frac{2}{3} \times \frac{3}{2} = 1 $.
-
Perkalian dengan Nol
Setiap bilangan rasional yang dikalikan dengan nol akan menghasilkan nol. Contoh: -
$ \frac{1}{2} \times 0 = 0 $
-
Bentuk Desimal Berulang
Bilangan rasional memiliki bentuk desimal yang berulang atau berhenti. Contoh: - $ \frac{1}{3} = 0,333… $
- $ \frac{1}{2} = 0,5 $
Contoh Bilangan Rasional
Berikut adalah beberapa contoh bilangan rasional yang sering ditemui dalam matematika:
-
Bilangan Bulat Positif dan Negatif
Contoh: 1, 2, -3, 4, -5, dan seterusnya. Semua bilangan bulat dapat dinyatakan dalam bentuk pecahan dengan penyebut 1, seperti 1 = 1/1, 2 = 2/1, dan -3 = -3/1. -
Pecahan Sederhana
Contoh: $ \frac{1}{2} $, $ \frac{3}{4} $, $ \frac{5}{6} $, $ \frac{-2}{3} $, dan $ \frac{7}{8} $. -
Desimal Berhenti
Contoh: 0,5 (sama dengan $ \frac{1}{2} $), 1,25 (sama dengan $ \frac{5}{4} $), dan 2,75 (sama dengan $ \frac{11}{4} $). -
Desimal Berulang
Contoh: 0,333… (sama dengan $ \frac{1}{3} $), 0,142857142857… (sama dengan $ \frac{1}{7} $), dan 1,666… (sama dengan $ \frac{5}{3} $). -
Persen dan Bagian dari Keseluruhan
Contoh: 25% (sama dengan $ \frac{25}{100} $), 50% (sama dengan $ \frac{50}{100} $), dan 75% (sama dengan $ \frac{75}{100} $). -
Bilangan yang Dapat Diubah Menjadi Pecahan
Contoh: 0,45 (sama dengan $ \frac{45}{100} $), 0,6 (sama dengan $ \frac{6}{10} $), dan 0,8 (sama dengan $ \frac{8}{10} $).
Perbedaan Bilangan Rasional dan Irasional
Meskipun keduanya termasuk dalam sistem bilangan real, bilangan rasional dan irasional memiliki perbedaan signifikan. Berikut adalah perbedaan utama antara keduanya:
| Kriteria | Bilangan Rasional | Bilangan Irasional |
|---|---|---|
| Bentuk | Dapat dinyatakan dalam bentuk pecahan $ \frac{a}{b} $, di mana $ a $ dan $ b $ adalah bilangan bulat dan $ b \neq 0 $. | Tidak dapat dinyatakan dalam bentuk pecahan $ \frac{a}{b} $, di mana $ a $ dan $ b $ adalah bilangan bulat dan $ b \neq 0 $. |
| Desimal | Memiliki bentuk desimal berhenti atau berulang. | Memiliki bentuk desimal tak berujung dan tidak berulang. |
| Contoh | 1/2, 0,5, 1,25, 0,333…, 25%. | √2, π, e, √3, √5. |
| Sifat | Tertutup terhadap operasi penjumlahan, perkalian, dan memiliki sifat komutatif, asosiatif, dan distributif. | Tidak tertutup terhadap operasi penjumlahan dan perkalian. |
Manfaat Memahami Bilangan Rasional
Memahami pengertian bilangan rasional memiliki banyak manfaat dalam kehidupan sehari-hari dan studi matematika. Beberapa manfaatnya meliputi:
-
Membantu dalam Perhitungan Keuangan
Dalam pengelolaan keuangan, bilangan rasional digunakan untuk menghitung pajak, diskon, dan bunga. Contohnya, menghitung potongan harga 20% dari harga barang yang bernilai Rp 100.000, yaitu Rp 20.000. -
Meningkatkan Kemampuan Analisis Data
Dalam ilmu statistik dan analisis data, bilangan rasional digunakan untuk menghitung rata-rata, proporsi, dan persentase. Contohnya, menghitung rata-rata nilai ujian siswa. -
Membantu dalam Pendidikan Matematika
Pemahaman tentang bilangan rasional merupakan dasar untuk mempelajari konsep-konsep matematika yang lebih kompleks, seperti aljabar, geometri, dan kalkulus. -
Meningkatkan Kemampuan Logika dan Pemecahan Masalah
Dengan memahami sifat-sifat bilangan rasional, kita dapat mengembangkan kemampuan logika dan pemecahan masalah dalam berbagai situasi. -
Menghindari Kesalahan dalam Perhitungan
Dengan memahami sifat-sifat bilangan rasional, kita dapat menghindari kesalahan dalam perhitungan matematika, terutama ketika melakukan operasi penjumlahan, pengurangan, perkalian, dan pembagian.
Kesimpulan
Pengertian bilangan rasional adalah konsep penting dalam matematika yang mengacu pada bilangan yang dapat dinyatakan dalam bentuk pecahan $ \frac{a}{b} $, di mana $ a $ dan $ b $ adalah bilangan bulat dan $ b \neq 0 $. Bilangan rasional mencakup berbagai jenis angka, termasuk bilangan bulat, pecahan, dan desimal berhenti atau berulang. Selain itu, bilangan rasional memiliki sifat-sifat khusus seperti tertutup terhadap operasi penjumlahan dan perkalian, serta memiliki sifat komutatif, asosiatif, dan distributif.
Memahami bilangan rasional tidak hanya membantu dalam studi matematika, tetapi juga dalam kehidupan sehari-hari, seperti perhitungan keuangan, analisis data, dan pemecahan masalah. Dengan pemahaman yang baik tentang bilangan rasional, kita dapat mengoptimalkan kemampuan matematika dan meningkatkan kualitas hidup melalui pengambilan keputusan yang lebih tepat.

















Komentar