Integral substitusi adalah salah satu metode dalam kalkulus yang digunakan untuk menyelesaikan integral yang tidak dapat diselesaikan secara langsung. Teknik ini sangat berguna ketika fungsi yang diintegrasikan memiliki bentuk kompleks atau mengandung variabel yang saling berkaitan. Dengan memahami cara menghitung integral substitusi, Anda akan lebih mudah menyelesaikan berbagai jenis soal matematika, terutama dalam bidang trigonometri dan aljabar.
Dalam konteks pendidikan, integral substitusi sering muncul dalam ujian nasional (UN) maupun ujian masuk perguruan tinggi. Contohnya, soal-soal seperti ∫cos³3x sin3x dx atau ∫sin³x cos²x dx sering kali membutuhkan teknik substitusi agar bisa diselesaikan. Oleh karena itu, pemahaman mendalam tentang integral substitusi sangat penting bagi siswa kelas 12 SMA, khususnya yang mengambil jurusan IPA.
Integral substitusi bekerja dengan mempermudah struktur fungsi yang diintegrasikan melalui substitusi variabel. Misalnya, jika kita memiliki fungsi yang mengandung turunan dari suatu fungsi lain, kita bisa mengganti bagian tersebut dengan variabel baru agar lebih sederhana. Metode ini tidak hanya membantu menyelesaikan soal, tetapi juga meningkatkan pemahaman tentang hubungan antara fungsi dan turunannya.
Apa Itu Integral Substitusi?
Integral substitusi adalah teknik matematika yang digunakan untuk menyelesaikan integral dengan mengganti bagian dari fungsi asli dengan variabel baru. Tujuannya adalah untuk menyederhanakan proses integrasi sehingga lebih mudah dikerjakan. Metode ini umumnya digunakan ketika fungsi yang diintegrasikan memiliki bentuk yang kompleks, seperti fungsi trigonometri, eksponensial, atau polinomial yang saling berkaitan.
Secara umum, integral substitusi bekerja dengan prinsip dasar bahwa jika ada fungsi f(g(x)) yang dikalikan dengan turunan dari g(x), maka kita bisa melakukan substitusi dengan memisalkan u = g(x). Setelah itu, kita akan mengubah dx menjadi du/dx, sehingga fungsi menjadi lebih sederhana dan dapat diintegrasikan.
Contoh sederhana dari integral substitusi adalah ∫2x cos(x² + 1) dx. Dalam kasus ini, kita bisa memisalkan u = x² + 1, sehingga du/dx = 2x. Dengan demikian, dx = du/2x. Kita kemudian mengganti x² + 1 dengan u dan 2x dx dengan du, sehingga integral menjadi ∫cos(u) du, yang jauh lebih mudah untuk diselesaikan.
Langkah-Langkah Menghitung Integral Substitusi
Menghitung integral substitusi memerlukan beberapa langkah yang harus dilakukan secara sistematis. Berikut adalah panduan lengkap untuk menyelesaikan integral substitusi:
-
Identifikasi Fungsi yang Akan Diintegrasikan
Pertama, perhatikan fungsi yang ingin Anda integrasikan. Cari bagian dari fungsi yang merupakan turunan dari bagian lain. Misalnya, jika Anda melihat fungsi seperti ∫5x sin(x²) dx, maka x² adalah bagian yang bisa dipermisalkan sebagai u. -
Buat Substitusi Variabel
Pilih bagian dari fungsi yang akan diganti dengan variabel baru. Misalnya, dalam ∫5x sin(x²) dx, Anda bisa membuat substitusi u = x². -
Hitung Turunan dari Variabel Baru
Setelah memilih variabel baru, hitung turunan dari variabel tersebut terhadap x. Dalam contoh di atas, jika u = x², maka du/dx = 2x. Dengan demikian, dx = du/(2x). -
Ganti Variabel dalam Fungsi Asli
Ganti semua bagian fungsi asli dengan variabel baru dan turunan yang telah dihitung. Dalam contoh ∫5x sin(x²) dx, setelah substitusi, fungsi menjadi ∫5x sin(u) * (du/2x). Bagian 5x dan 2x akan saling mencoret, sehingga tersisa ∫(5/2) sin(u) du. -
Selesaikan Integral yang Sederhana
Setelah fungsi disederhanakan, selesaikan integral menggunakan rumus dasar. Dalam contoh di atas, ∫sin(u) du = -cos(u) + C. Jadi, hasil akhirnya adalah -(5/2) cos(u) + C. -
Kembalikan Variabel ke Bentuk Awal
Terakhir, ganti variabel baru (u) kembali ke bentuk awal (x² dalam contoh ini). Hasil akhirnya adalah -(5/2) cos(x²) + C.
Contoh Soal Integral Substitusi
Untuk memperjelas pemahaman, berikut adalah beberapa contoh soal integral substitusi beserta penyelesaiannya:
Contoh 1: ∫cos³3x sin3x dx
Langkah-langkah penyelesaian:
1. Misalkan v = cos3x
2. Turunkan v: dv/dx = -3 sin3x → dx = dv/(-3 sin3x)
3. Substitusi ke dalam integral: ∫v³ * sin3x * (dv/(-3 sin3x))
4. Sederhanakan: ∫-v³/3 dv
5. Integralkan: -1/3 * v⁴/4 + C = -v⁴/12 + C
6. Ganti v kembali: -cos⁴3x/12 + C
Hasil akhir: -cos⁴3x/12 + C
Contoh 2: ∫sin³x cos²x dx
Langkah-langkah penyelesaian:
1. Gunakan identitas trigonometri: sin²x = 1 – cos²x
2. Ubah integral menjadi: ∫(1 – cos²x) sinx cos²x dx
3. Bagi menjadi dua integral: ∫sinx cos²x dx – ∫sinx cos⁴x dx
4. Substitusi u = cosx, du = -sinx dx
5. Selesaikan kedua integral: -∫u² du + ∫u⁴ du = -u³/3 + u⁵/5 + C
6. Ganti u kembali: -cos³x/3 + cos⁵x/5 + C
Hasil akhir: -cos³x/3 + cos⁵x/5 + C
Tips dan Trik dalam Menghitung Integral Substitusi
Menghitung integral substitusi membutuhkan latihan dan pemahaman yang baik tentang turunan dan fungsi. Berikut beberapa tips dan trik yang bisa membantu Anda:
- Kenali Pola Fungsi: Pastikan Anda mengenali pola fungsi yang bisa disubstitusi. Contohnya, jika ada fungsi yang mengandung turunan dari suatu fungsi lain, itu bisa menjadi petunjuk untuk substitusi.
- Gunakan Identitas Trigonometri: Dalam soal trigonometri, identitas seperti sin²x + cos²x = 1 sering kali membantu menyederhanakan fungsi sebelum melakukan substitusi.
- Latihan Secara Berkala: Latihan rutin dengan berbagai jenis soal akan membantu Anda lebih cepat mengenali strategi substitusi yang tepat.
- Periksa Kembali Hasil: Setelah menyelesaikan integral, periksa kembali apakah hasil yang diperoleh sudah sesuai dengan aturan turunan. Ini membantu menghindari kesalahan dalam pengerjaan.
Manfaat Integral Substitusi dalam Pendidikan dan Karier
Integral substitusi bukan hanya sekadar materi matematika yang harus dikuasai oleh siswa, tetapi juga memiliki manfaat nyata dalam berbagai bidang studi dan karier. Dalam ilmu fisika, misalnya, integral digunakan untuk menghitung luasan benda berbentuk kurva, kecepatan, dan energi. Dalam ekonomi, integral bisa digunakan untuk menghitung total biaya produksi atau pendapatan marginal.
Selain itu, pemahaman tentang integral substitusi sangat penting bagi mahasiswa yang ingin mengambil jurusan teknik, matematika, atau ilmu komputer. Banyak mata kuliah lanjutan seperti kalkulus lanjut, persamaan diferensial, dan analisis numerik membutuhkan kemampuan dasar dalam menyelesaikan integral.
Kesimpulan
Integral substitusi adalah teknik penting dalam kalkulus yang membantu menyelesaikan berbagai jenis integral yang kompleks. Dengan memahami langkah-langkah dasar dan latihan secara rutin, Anda akan mampu menyelesaikan soal-soal integral dengan lebih mudah. Baik dalam ujian nasional maupun dalam studi lanjut, kemampuan menghitung integral substitusi sangat berguna dan memberikan dasar kuat dalam memahami konsep-konsep matematika yang lebih rumit.
Dengan mempelajari dan menguasai integral substitusi, Anda tidak hanya meningkatkan kemampuan matematika, tetapi juga mempersiapkan diri untuk berbagai bidang studi dan karier yang membutuhkan analisis kuantitatif. Mulailah dengan latihan soal sederhana, dan secara bertahap tingkatkan kesulitan agar Anda semakin percaya diri dalam menghadapi tantangan matematika.



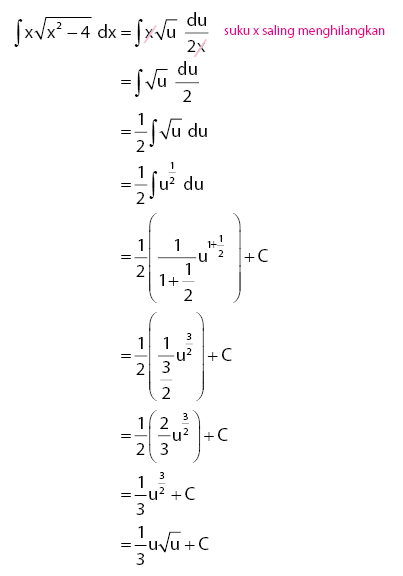















Komentar