Gerak Lurus Beraturan (GLB) adalah salah satu konsep dasar dalam ilmu fisika yang sering diajarkan di sekolah menengah. Meskipun terdengar sederhana, GLB memiliki peran penting dalam memahami bagaimana benda bergerak dalam keadaan stabil tanpa mengalami percepatan. Pemahaman tentang GLB tidak hanya berguna untuk ujian akademis, tetapi juga bisa diterapkan dalam kehidupan sehari-hari.
Dalam dunia nyata, GLB jarang terjadi karena adanya faktor-faktor seperti gesekan, hambatan udara, atau perubahan kecepatan. Namun, dalam lingkungan tertentu seperti luar angkasa, GLB dapat terjadi dengan sempurna. Konsep ini sangat relevan dalam bidang transportasi, teknologi, dan bahkan dalam pengembangan sistem otomatis.
Artikel ini akan membahas secara lengkap tentang pengertian GLB, rumus-rumus yang digunakan, contoh penerapan dalam kehidupan nyata, serta beberapa soal latihan untuk memperdalam pemahaman. Dengan informasi yang jelas dan mudah dipahami, pembaca akan mendapatkan wawasan menyeluruh tentang GLB.
Apa Itu Gerak Lurus Beraturan (GLB)?
Gerak Lurus Beraturan (GLB) adalah gerakan suatu benda yang berlangsung pada lintasan lurus dengan kecepatan yang tetap. Artinya, benda tersebut tidak mengalami percepatan atau perlambatan selama bergerak. Dalam konteks fisika, GLB merupakan salah satu bentuk gerak yang paling sederhana karena hanya melibatkan dua variabel utama, yaitu kecepatan dan waktu.
Kunci dari GLB adalah bahwa kecepatan benda tidak berubah sepanjang waktu. Jika sebuah benda bergerak dengan kecepatan 10 m/s, maka setiap detiknya benda tersebut akan menempuh jarak sejauh 10 meter. Hal ini membuat GLB menjadi model ideal untuk mempelajari gerak dalam kondisi ideal tanpa gangguan eksternal.
Secara matematis, GLB dapat dinyatakan dengan rumus sederhana seperti:
$$
v = \frac{s}{t}
$$
di mana:
– $ v $ adalah kecepatan (dalam satuan meter per detik),
– $ s $ adalah jarak tempuh,
– $ t $ adalah waktu.
Rumus ini menunjukkan hubungan langsung antara jarak, kecepatan, dan waktu. Dengan memahami rumus ini, kita dapat menghitung kecepatan benda, jarak yang ditempuh, atau waktu yang dibutuhkan untuk menempuh jarak tertentu.
Ciri-Ciri Gerak Lurus Beraturan (GLB)
Untuk lebih memahami GLB, berikut beberapa ciri-ciri utamanya:
- Lintasan Lurus: Benda bergerak dalam garis lurus tanpa mengalami belokan.
- Kecepatan Tetap: Kecepatan benda tidak berubah sepanjang waktu, artinya tidak ada percepatan.
- Percepatan Nol: Karena kecepatan tetap, percepatan benda bernilai nol.
- Jarak Tempuh Sama Tiap Satuan Waktu: Jika benda bergerak selama 1 detik, maka jarak yang ditempuh sama tiap detiknya.
Contoh nyata dari GLB adalah mobil yang bergerak di jalan tol dengan kecepatan tetap. Saat speedometer menunjukkan angka yang stabil, itu berarti mobil tersebut sedang bergerak dalam kondisi GLB.
Grafik Gerak Lurus Beraturan (GLB)
Grafik merupakan alat visual yang sangat berguna untuk memahami GLB. Berikut adalah beberapa jenis grafik yang umum digunakan:
-
Grafik Kecepatan vs. Waktu
Grafik ini menunjukkan bahwa kecepatan benda tetap sepanjang waktu. Garis yang terbentuk adalah garis lurus horizontal. -
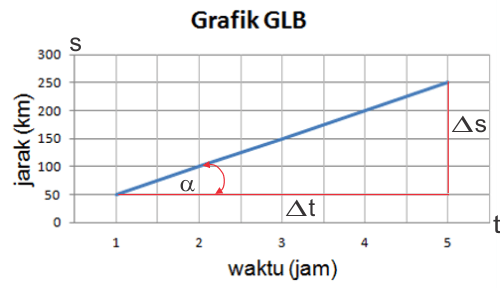
Grafik Posisi vs. Waktu
Pada grafik ini, posisi benda meningkat secara linear terhadap waktu. Bentuk garisnya adalah garis lurus miring. -
Grafik Percepatan vs. Waktu
Karena percepatan benda bernilai nol, garis pada grafik ini adalah garis horizontal di angka nol.
Grafik-grafik ini membantu dalam memvisualisasikan bagaimana benda bergerak dalam kondisi GLB.
Penerapan Gerak Lurus Beraturan (GLB) dalam Kehidupan Sehari-Hari
Meskipun GLB jarang terjadi dalam kehidupan nyata, konsep ini memiliki banyak penerapan dalam berbagai bidang. Berikut adalah beberapa contohnya:
-
Transportasi Darat
Mobil yang bergerak di jalan tol dengan kecepatan tetap adalah contoh nyata dari GLB. Speedometer yang menunjukkan angka stabil menandakan bahwa mobil sedang bergerak dalam kondisi GLB. -
Transportasi Laut
Kapal laut yang berlayar di laut lepas dengan kecepatan konstan juga merupakan contoh GLB. Ketika kapal akan berlabuh, kecepatannya berubah, tetapi selama perjalanan, kecepatannya tetap. -
Transportasi Udara
Pesawat terbang yang sudah mencapai ketinggian stabil dan bergerak lurus dengan kecepatan tetap juga mengalami GLB. Ini terjadi sebelum pesawat mulai turun menuju tujuan.
Selain itu, GLB juga digunakan dalam desain sistem otomatis, seperti robot atau mesin industri yang bekerja dengan kecepatan konstan.
Rumus Gerak Lurus Beraturan (GLB)
Sebagai bentuk matematis dari GLB, rumus-rumus berikut digunakan untuk menghitung kecepatan, jarak, dan waktu:
- Rumus Kecepatan Sesaat
$$
v = \frac{s}{t}
$$
di mana: - $ v $ = kecepatan sesaat (m/s)
- $ s $ = jarak perpindahan (m)
-
$ t $ = waktu (s)
-
Rumus Kecepatan Rata-Rata
$$
\bar{v} = \frac{\Delta s}{\Delta t}
$$
di mana: - $ \bar{v} $ = kecepatan rata-rata (m/s)
- $ \Delta s $ = perubahan posisi (m)
- $ \Delta t $ = perubahan waktu (s)
Rumus-rumus ini sangat berguna dalam menyelesaikan berbagai masalah fisika yang berkaitan dengan GLB.
Contoh Soal Gerak Lurus Beraturan (GLB)
Berikut adalah beberapa contoh soal yang menggunakan konsep GLB:
- Soal 1
Pesawat jet bergerak menuju bulan dengan data sebagai berikut:
| Waktu (jam) | Jarak (km) |
|————-|————|
| 1 | 500 |
| 2 | 1000 |
| 3 | 1500 |
| 4 | 2000 |
| 5 | 2500 |
Hitung kecepatan saat $ t = 3 $ jam dan kecepatan rata-ratanya!
Penyelesaian:
Kecepatan sesaat:
$$
v = \frac{1500}{3} = 500 \, \text{km/jam}
$$
Kecepatan rata-rata:
$$
\bar{v} = \frac{2500 – 500}{5 – 1} = \frac{2000}{4} = 500 \, \text{km/jam}
$$
- Soal 2
Mobil A dan B bergerak saling mendekati dengan jarak awal 420 m. Kecepatan mobil A adalah 40 m/s dan mobil B adalah 10 m/s. Tentukan titik pertemuan kedua mobil tersebut!
Penyelesaian:
Misalkan jarak yang ditempuh mobil A adalah $ x $, maka jarak yang ditempuh mobil B adalah $ 420 – x $.
Waktu tempuh sama, sehingga:
$$
\frac{x}{40} = \frac{420 – x}{10}
$$
Selesaikan persamaan:
$$
10x = 1680 – 40x \Rightarrow 50x = 1680 \Rightarrow x = 33.6 \, \text{m}
$$
Jadi, titik pertemuan berada 33.6 meter dari posisi awal mobil A.
Kesimpulan
Gerak Lurus Beraturan (GLB) adalah konsep dasar dalam fisika yang menjelaskan gerakan benda dengan kecepatan tetap. Meskipun jarang terjadi dalam kehidupan nyata, GLB memiliki banyak penerapan dalam transportasi, teknologi, dan desain sistem. Dengan memahami rumus dan contoh soal, kita dapat menguasai konsep ini dengan baik. Semoga artikel ini memberikan pengetahuan yang bermanfaat bagi para pembaca.



















Komentar