Dalam dunia fisika, konsep tentang gerak benda sangat penting untuk dipahami. Salah satu aspek penting dalam gerak benda adalah perlambatan. Perlambatan merupakan salah satu bentuk percepatan yang terjadi ketika kecepatan suatu benda menurun seiring berjalannya waktu. Pemahaman tentang perlambatan tidak hanya berguna dalam studi fisika, tetapi juga dalam kehidupan sehari-hari, seperti pengereman kendaraan atau melempar bola ke atas.
Rumus perlambatan menjadi alat penting untuk menghitung seberapa cepat kecepatan suatu benda melambat. Dengan memahami rumus ini, kita dapat menganalisis berbagai situasi fisika yang melibatkan perubahan kecepatan. Tidak hanya itu, pemahaman tentang perlambatan juga membantu dalam merancang sistem keselamatan kendaraan, menghitung jarak tempuh, atau bahkan dalam olahraga seperti lompat jauh atau lempar lembing.
Artikel ini akan membahas secara mendalam tentang pengertian perlambatan, rumusnya, serta contoh nyata dari perlambatan dalam kehidupan sehari-hari. Selain itu, artikel ini juga akan menjelaskan bagaimana rumus perlambatan digunakan dalam berbagai situasi, termasuk dalam gerak lurus berubah beraturan (GLBB). Dengan informasi yang lengkap dan terstruktur, pembaca akan memperoleh wawasan yang memadai tentang perlambatan dalam konteks fisika.
Apa Itu Perlambatan?
Perlambatan adalah istilah yang digunakan untuk menggambarkan penurunan kecepatan suatu benda seiring waktu. Secara teknis, perlambatan merupakan bentuk percepatan negatif, karena arahnya berlawanan dengan arah kecepatan benda. Misalnya, jika sebuah mobil sedang bergerak ke depan, maka perlambatan terjadi ketika mobil tersebut mulai melambat karena pengereman.
Dalam ilmu fisika, percepatan didefinisikan sebagai perubahan kecepatan dalam satuan waktu. Jika kecepatan meningkat, maka percepatan bernilai positif. Namun, jika kecepatan menurun, maka percepatan bernilai negatif, yang disebut dengan perlambatan. Oleh karena itu, perlambatan sering disebut sebagai “percepatan negatif” dalam konteks fisika.
Contoh sederhana dari perlambatan adalah saat seseorang mengerem sepeda. Ketika sepeda bergerak dengan kecepatan tertentu, tindakan mengerem menyebabkan kecepatan sepeda berkurang. Proses ini menunjukkan bahwa perlambatan terjadi karena adanya gaya yang bekerja berlawanan dengan arah gerak.
Pemahaman tentang perlambatan sangat penting dalam banyak bidang, seperti teknik, olahraga, dan transportasi. Dalam teknik, misalnya, penghitungan perlambatan diperlukan untuk merancang sistem pengereman yang efektif. Dalam olahraga, pemahaman tentang perlambatan membantu atlet mengoptimalkan performa mereka, terutama dalam olahraga yang melibatkan perubahan kecepatan, seperti sepak bola atau renang.
Rumus Perlambatan dalam Fisika
Rumus perlambatan dalam fisika digunakan untuk menghitung seberapa cepat kecepatan suatu benda berkurang. Secara umum, rumus ini mirip dengan rumus percepatan, tetapi dengan nilai yang negatif karena kecepatan akhir lebih kecil daripada kecepatan awal.
Rumus dasar untuk menghitung perlambatan adalah:
$$
a = \frac{v_2 – v_1}{t}
$$
Di mana:
– $ a $ adalah perlambatan (dalam satuan m/s²)
– $ v_2 $ adalah kecepatan akhir (dalam satuan m/s)
– $ v_1 $ adalah kecepatan awal (dalam satuan m/s)
– $ t $ adalah waktu tempuh (dalam satuan detik)
Karena perlambatan terjadi ketika kecepatan akhir lebih kecil dari kecepatan awal, maka hasil perhitungan akan selalu bernilai negatif. Contohnya, jika sebuah mobil bergerak dengan kecepatan 30 m/s dan berhenti dalam waktu 5 detik, maka perlambatannya dapat dihitung sebagai berikut:
$$
a = \frac{0 – 30}{5} = -6 \, \text{m/s}^2
$$
Nilai negatif menunjukkan bahwa kecepatan mobil berkurang seiring waktu, sehingga terjadi perlambatan.
Selain rumus dasar tersebut, dalam gerak lurus berubah beraturan (GLBB), ada beberapa rumus tambahan yang bisa digunakan, tergantung pada variabel yang diketahui. Misalnya, jika kecepatan awal, kecepatan akhir, dan jarak tempuh diketahui, maka rumus berikut dapat digunakan:
$$
v_2^2 = v_1^2 + 2aS
$$
Di mana:
– $ S $ adalah jarak tempuh (dalam satuan meter)
Rumus ini sangat berguna dalam situasi di mana waktu tidak diketahui, tetapi jarak tempuh dan kecepatan awal serta akhir diketahui. Contohnya, jika seseorang melempar bola ke atas dan bola mencapai ketinggian tertentu sebelum jatuh kembali, rumus ini dapat digunakan untuk menghitung perlambatan akibat gravitasi bumi.
Dengan memahami rumus-rumus ini, kita dapat menganalisis berbagai situasi fisika yang melibatkan perlambatan, baik dalam kehidupan sehari-hari maupun dalam studi ilmu fisika.
Contoh Peristiwa Perlambatan dalam Kehidupan Sehari-Hari
Perlambatan tidak hanya terjadi dalam konteks fisika teoritis, tetapi juga sering kita temui dalam kehidupan sehari-hari. Beberapa contoh nyata dari perlambatan antara lain:
1. Pengereman Kendaraan
Salah satu contoh paling umum dari perlambatan adalah saat kendaraan seperti mobil, motor, atau kereta mengerem. Saat pengemudi menekan rem, kendaraan mengalami perlambatan karena gaya gesekan antara ban dan permukaan jalan. Proses ini membuat kecepatan kendaraan berkurang hingga akhirnya berhenti. Perlambatan ini sangat penting dalam keselamatan berkendara, karena tanpa pengereman yang efektif, kecelakaan bisa terjadi.
2. Melempar Bola ke Atas
Ketika seseorang melempar bola ke atas, bola tersebut awalnya memiliki kecepatan positif. Namun, karena pengaruh gravitasi bumi, bola mengalami perlambatan. Kecepatan bola terus berkurang hingga mencapai titik tertinggi, setelah itu bola mulai jatuh kembali ke bawah. Proses ini menunjukkan bahwa perlambatan terjadi karena gaya gravitasi bekerja berlawanan dengan arah gerak bola.
3. Bersepeda di Turunan
Ketika seorang pengendara sepeda turun dari bukit, kecepatan sepeda meningkat karena gravitasi. Namun, saat naik bukit, kecepatan sepeda berkurang karena usaha yang dilakukan untuk mengatasi gaya gravitasi. Proses ini menunjukkan bahwa perlambatan juga bisa terjadi saat bersepeda di lereng yang curam.
4. Mendarat Setelah Melompat
Ketika seseorang melompat dari ketinggian, misalnya dari panggung atau atap, kecepatan tubuhnya meningkat karena gravitasi. Namun, saat tubuh menyentuh tanah, kecepatan berkurang drastis. Proses ini menunjukkan bahwa perlambatan terjadi karena gaya yang bekerja pada tubuh saat mendarat, seperti gaya gesekan dan gaya normal.
5. Menghentikan Gerakan Bola dalam Olahraga
Dalam olahraga seperti sepak bola atau basket, pemain sering kali harus menghentikan gerakan bola. Misalnya, saat seorang pemain menendang bola, bola bergerak dengan kecepatan tinggi. Namun, saat bola dihentikan oleh kiper atau pemain lain, bola mengalami perlambatan. Proses ini menunjukkan bahwa perlambatan juga terjadi dalam aktivitas olahraga.
Dengan memahami contoh-contoh ini, kita dapat melihat bahwa perlambatan tidak hanya terjadi dalam konteks fisika, tetapi juga dalam berbagai situasi nyata yang kita alami sehari-hari. Pemahaman tentang perlambatan membantu kita memahami cara kerja alam dan bagaimana kita dapat menggunakannya dalam kehidupan sehari-hari.
Penerapan Rumus Perlambatan dalam Gerak Lurus Berubah Beraturan (GLBB)
Dalam studi fisika, gerak lurus berubah beraturan (GLBB) adalah gerak benda yang bergerak pada lintasan lurus dengan percepatan yang tetap. Dalam GLBB, benda dapat mengalami percepatan positif (dipercepat) atau percepatan negatif (diperlambat). Rumus perlambatan dalam GLBB digunakan untuk menghitung perubahan kecepatan benda yang melambat seiring waktu.
Beberapa rumus utama dalam GLBB yang digunakan untuk menghitung perlambatan adalah:
- Rumus kecepatan akhir:
$$
v_t = v_0 + at
$$
Di mana: - $ v_t $: kecepatan akhir (m/s)
- $ v_0 $: kecepatan awal (m/s)
- $ a $: percepatan (m/s²)
-
$ t $: waktu (s)
-
Rumus kecepatan kuadrat:
$$
v_t^2 = v_0^2 + 2aS
$$
Di mana: -
$ S $: jarak tempuh (m)
-
Rumus jarak tempuh:
$$
S = v_0 t + \frac{1}{2} a t^2
$$
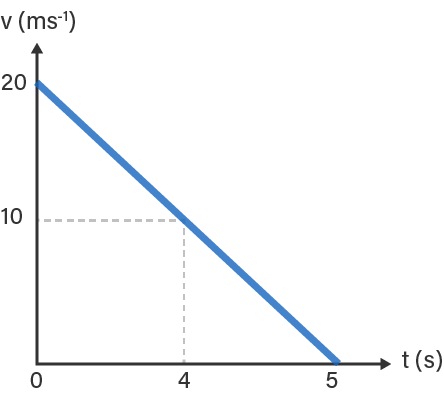
Dalam kasus perlambatan, nilai percepatan ($ a $) akan bernilai negatif karena kecepatan benda berkurang. Contohnya, jika sebuah mobil bergerak dengan kecepatan awal 20 m/s dan berhenti dalam waktu 5 detik, maka perlambatannya dapat dihitung sebagai berikut:
$$
a = \frac{v_t – v_0}{t} = \frac{0 – 20}{5} = -4 \, \text{m/s}^2
$$
Setelah mengetahui nilai percepatan, kita dapat menggunakan rumus lain untuk menghitung jarak tempuh atau kecepatan akhir. Misalnya, dengan menggunakan rumus kecepatan kuadrat:
$$
v_t^2 = v_0^2 + 2aS \
0^2 = 20^2 + 2(-4)S \
0 = 400 – 8S \
8S = 400 \
S = 50 \, \text{m}
$$
Dengan demikian, jarak tempuh mobil sebelum berhenti adalah 50 meter. Penerapan rumus ini sangat berguna dalam berbagai situasi, seperti perencanaan jalan raya, desain sistem pengereman, atau analisis gerak dalam olahraga.
Contoh Soal dan Pembahasan tentang Perlambatan
Untuk memperkuat pemahaman tentang rumus perlambatan, berikut ini beberapa contoh soal beserta pembahasan:
Contoh 1: Mobil yang Berhenti
Sebuah mobil bergerak dengan kecepatan awal 30 m/s. Setelah melakukan pengereman, mobil berhenti dalam waktu 5 detik. Hitunglah besar perlambatan mobil tersebut!
Penyelesaian:
Diketahui:
– Kecepatan awal ($ v_0 $) = 30 m/s
– Kecepatan akhir ($ v_t $) = 0 m/s
– Waktu ($ t $) = 5 s
Menggunakan rumus:
$$
a = \frac{v_t – v_0}{t} = \frac{0 – 30}{5} = -6 \, \text{m/s}^2
$$
Jadi, besar perlambatan mobil adalah $ -6 \, \text{m/s}^2 $.
Contoh 2: Bola yang Dilempar ke Atas
Bola dilempar ke atas dengan kecepatan awal 20 m/s. Hitunglah waktu yang dibutuhkan bola untuk mencapai titik tertinggi dan kecepatan akhirnya!
Penyelesaian:
Diketahui:
– Kecepatan awal ($ v_0 $) = 20 m/s
– Percepatan ($ a $) = -9,8 m/s² (karena gravitasi bumi)
– Kecepatan akhir ($ v_t $) = 0 m/s (di titik tertinggi)
Menggunakan rumus:
$$
v_t = v_0 + at \
0 = 20 + (-9,8)t \
t = \frac{20}{9,8} \approx 2,04 \, \text{s}
$$
Jadi, waktu yang dibutuhkan bola untuk mencapai titik tertinggi adalah sekitar 2,04 detik.
Contoh 3: Kereta yang Melambat
Kereta bergerak dengan kecepatan awal 50 m/s dan melambat hingga berhenti dalam waktu 10 detik. Hitunglah jarak tempuh kereta sebelum berhenti!
Penyelesaian:
Diketahui:
– Kecepatan awal ($ v_0 $) = 50 m/s
– Kecepatan akhir ($ v_t $) = 0 m/s
– Waktu ($ t $) = 10 s
Menggunakan rumus:
$$
a = \frac{v_t – v_0}{t} = \frac{0 – 50}{10} = -5 \, \text{m/s}^2
$$
Kemudian, menggunakan rumus jarak tempuh:
$$
S = v_0 t + \frac{1}{2} a t^2 \
S = 50(10) + \frac{1}{2}(-5)(10)^2 \
S = 500 – 250 = 250 \, \text{m}
$$
Jadi, jarak tempuh kereta sebelum berhenti adalah 250 meter.
Dengan contoh soal dan pembahasan ini, kita dapat melihat bagaimana rumus perlambatan digunakan dalam berbagai situasi nyata. Pemahaman tentang rumus ini sangat penting dalam memahami gerak benda yang melambat, baik dalam kehidupan sehari-hari maupun dalam studi ilmu fisika.



















Komentar