Pahami Rumus Kuartil dan Cara Menghitungnya dengan Mudah
Dalam dunia statistik, kuartil menjadi salah satu konsep penting yang digunakan untuk memahami distribusi data. Kuartil membantu kita membagi data menjadi empat bagian yang sama besar, sehingga memudahkan analisis dan pengambilan keputusan berdasarkan data. Dengan memahami rumus kuartil, Anda tidak hanya akan mampu menghitung nilai-nilai tersebut secara akurat, tetapi juga dapat memahami makna dari setiap kuartil dalam konteks data yang dianalisis.
Kuartil terdiri dari tiga jenis utama: kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3). Q1 adalah batas antara 25% data terendah dan 75% data tertinggi. Q2 merupakan median atau nilai tengah dari seluruh data, sedangkan Q3 adalah batas antara 75% data terendah dan 25% data tertinggi. Dengan memahami kuartil, Anda bisa mengetahui sebaran data, identifikasi outlier, serta membuat prediksi yang lebih tepat.
Artikel ini akan membahas secara mendetail tentang rumus kuartil, cara menghitungnya baik untuk data tunggal maupun data berkelompok, serta contoh soal yang mudah dipahami. Selain itu, kami juga akan menjelaskan manfaat dan penerapan kuartil dalam berbagai bidang seperti pendidikan, ekonomi, dan kesehatan. Dengan informasi lengkap ini, Anda akan memiliki pemahaman yang kuat tentang kuartil dan kemampuan untuk menerapkannya dalam situasi nyata.
Apa Itu Kuartil?
Kuartil adalah nilai yang membagi kumpulan data yang telah diurutkan menjadi empat bagian yang sama besar. Setiap bagian mewakili 25% dari total data. Dengan demikian, kuartil memberikan gambaran yang lebih jelas tentang sebaran data dan membantu dalam pengambilan keputusan yang lebih akurat.
Secara umum, ada tiga jenis kuartil:
– Kuartil Pertama (Q1): Memisahkan 25% data terendah dari sisanya.
– Kuartil Kedua (Q2): Sama dengan median, membagi data menjadi dua bagian sama besar.
– Kuartil Ketiga (Q3): Memisahkan 75% data terendah dari 25% data tertinggi.
Kuartil sangat berguna dalam analisis statistik karena memberikan informasi tentang sebaran data, termasuk identifikasi outlier dan perhitungan interquartile range (IQR), yang merupakan ukuran sebaran data yang lebih stabil dibandingkan range biasa.
Rumus Kuartil Data Tunggal
Untuk menghitung kuartil dari data tunggal, langkah-langkahnya adalah sebagai berikut:
- Urutkan data: Pastikan data diurutkan dari nilai terkecil hingga terbesar.
- Tentukan posisi kuartil: Gunakan rumus berikut untuk menemukan posisi kuartil:
- Q1 = (n + 1) / 4
- Q2 = (n + 1) / 2
- Q3 = 3(n + 1) / 4
Di mana n adalah jumlah data.
- Hitung nilai kuartil:
- Jika posisi kuartil adalah bilangan bulat, maka nilai kuartil adalah nilai pada posisi tersebut.
- Jika posisi kuartil bukan bilangan bulat, lakukan interpolasi antara dua nilai data yang berdekatan.
Contoh Soal:
Misalkan data adalah: 4, 4, 5, 7, 8, 8, 8, 9, 10, 11, 11
Jumlah data (n) = 11
- Q1 = (11 + 1) / 4 = 3 → Nilai pada posisi ke-3 adalah 5
- Q2 = (11 + 1) / 2 = 6 → Nilai pada posisi ke-6 adalah 8
- Q3 = 3(11 + 1) / 4 = 9 → Nilai pada posisi ke-9 adalah 10
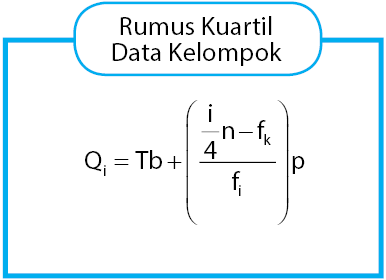
Rumus Kuartil Data Berkelompok
Untuk data berkelompok, perhitungan kuartil lebih kompleks karena data disajikan dalam bentuk interval. Berikut langkah-langkahnya:
- Buat tabel frekuensi kumulatif: Hitung frekuensi kumulatif dari setiap interval.
- Tentukan letak kuartil: Gunakan rumus:
-
Qi = (i * n) / 4
Di manaiadalah 1, 2, atau 3 untuk Q1, Q2, dan Q3. -
Cari kelas kuartil: Kelas kuartil adalah kelas yang memuat nilai kuartil sesuai dengan letaknya.
- Gunakan rumus kuartil:
- Q = L + ((n/4 – F) / f) * c
Di mana:- L = tepi bawah kelas kuartil
- F = frekuensi kumulatif sebelum kelas kuartil
- f = frekuensi kelas kuartil
- c = panjang kelas interval
Contoh Soal:
Misalkan data berat badan siswa kelas VII seperti berikut:
| Berat Badan | Frekuensi |
|---|---|
| 41–45 | 9 |
| 46–50 | 12 |
| 51–55 | 10 |
| 56–60 | 8 |
Jumlah data (n) = 39
- Q1 = (1 * 39) / 4 = 9.75 → Letak Q1 berada di kelas 41–45
- L = 41 – 0.5 = 40.5
- F = 0 (frekuensi kumulatif sebelum kelas 41–45)
- f = 9
- c = 5
Maka:
– Q1 = 40.5 + ((9.75 – 0) / 9) * 5 = 40.5 + 5.42 = 45.92
Manfaat dan Penerapan Kuartil
Kuartil memiliki banyak manfaat dalam berbagai bidang, antara lain:
- Ekonomi: Digunakan untuk menganalisis distribusi pendapatan dan kekayaan.
- Pendidikan: Membantu menilai prestasi siswa dan membandingkan kinerja antar sekolah.
- Kesehatan: Memantau pertumbuhan anak dan mengidentifikasi masalah kesehatan.
- Pemasaran: Segmentasi pasar dan memahami perilaku konsumen.
Dengan memahami kuartil, Anda bisa mengambil keputusan yang lebih informatif dan akurat berdasarkan data yang tersedia.
Kesimpulan
Kuartil adalah alat statistik yang sangat berguna untuk memahami sebaran data dan membuat keputusan yang lebih tepat. Dengan mempelajari rumus kuartil dan cara menghitungnya, baik untuk data tunggal maupun data berkelompok, Anda akan memiliki kemampuan untuk menganalisis data secara efektif. Artikel ini telah memberikan penjelasan lengkap tentang kuartil, mulai dari definisi, rumus, contoh soal, hingga penerapan dalam berbagai bidang. Dengan pemahaman ini, Anda siap menerapkan kuartil dalam situasi nyata dan meningkatkan kualitas analisis data Anda.
Kategori: Pendidikan & Ilmu Pengetahuan



















Komentar