Rumus Luas Selimut Kerucut dan Cara Menghitungnya dengan Mudah

Kerucut adalah salah satu bangun ruang yang sering kita temui dalam kehidupan sehari-hari, mulai dari topi ulang tahun hingga es krim cone. Namun, apakah kamu tahu bahwa di balik bentuknya yang sederhana, kerucut memiliki rumus matematika yang cukup menarik? Salah satu hal penting yang perlu dipahami dalam mempelajari kerucut adalah rumus luas selimut kerucut.

Selimut kerucut merupakan bagian melengkung yang mengelilingi alas kerucut. Dalam matematika, menghitung luas selimut kerucut tidak terlalu sulit jika kita memahami konsep dasarnya. Dengan rumus yang tepat, kita bisa menghitung luas selimut kerucut hanya dengan beberapa langkah sederhana.

Tidak hanya itu, pemahaman tentang rumus luas selimut kerucut juga sangat berguna dalam berbagai situasi nyata, seperti membuat topi kerucut atau menentukan ukuran bahan yang dibutuhkan untuk membuat sebuah kerucut. Oleh karena itu, artikel ini akan membahas secara lengkap tentang rumus luas selimut kerucut, cara menghitungnya, serta contoh soal yang bisa membantu kamu memahami konsep tersebut.

Apa Itu Kerucut?

Kerucut adalah bangun ruang tiga dimensi yang memiliki dua sisi utama, yaitu sisi alas yang berbentuk lingkaran dan sisi selimut yang melengkung. Kerucut juga memiliki satu titik puncak di atas sisi alasnya. Bentuknya mirip dengan cone ice cream yang sering kita lihat.

Secara geometris, kerucut dapat didefinisikan sebagai limas dengan alas berbentuk lingkaran. Karena memiliki bentuk yang unik, kerucut sering digunakan dalam berbagai bidang, baik dalam ilmu matematika maupun dalam kehidupan sehari-hari.

Unsur-unsur Kerucut

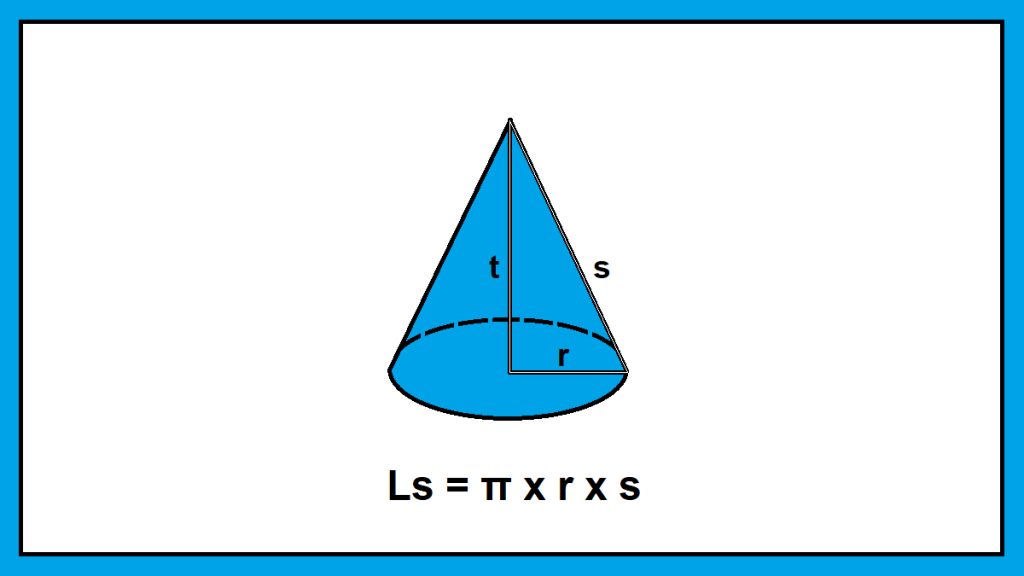
Sebelum masuk ke rumus luas selimut kerucut, penting untuk memahami unsur-unsur utama dari kerucut:

1. Alas: Sisi bawah kerucut yang berbentuk lingkaran.
2. Puncak: Titik teratas dari kerucut.
3. Tinggi (t): Jarak dari puncak kerucut ke pusat lingkaran alas.
4. Jari-jari (r): Jarak dari pusat lingkaran alas ke tepi lingkaran.
5. Garis pelukis (s): Garis yang menghubungkan puncak kerucut dengan tepi lingkaran alas. Garis ini juga disebut sebagai apotema.
6. Selimut: Sisi melengkung yang mengelilingi kerucut.

Dari keenam unsur ini, garis pelukis (s) dan jari-jari (r) menjadi komponen utama dalam rumus luas selimut kerucut.

Rumus Luas Selimut Kerucut

Rumus untuk menghitung luas selimut kerucut adalah:

$$
L = \pi \times r \times s
$$

Keterangan:
– $ L $ = Luas selimut kerucut
– $ \pi $ = Konstanta pi (sekitar 3,14 atau $ \frac{22}{7} $)
– $ r $ = Jari-jari alas kerucut
– $ s $ = Panjang garis pelukis (apotema)

Rumus ini didasarkan pada fakta bahwa selimut kerucut berbentuk juring lingkaran. Oleh karena itu, luas selimut dapat dihitung dengan mengalikan keliling lingkaran (dengan jari-jari $ r $) dengan panjang garis pelukis ($ s $).

Cara Menghitung Luas Selimut Kerucut

Berikut langkah-langkah praktis untuk menghitung luas selimut kerucut:

1. Tentukan nilai jari-jari (r): Jari-jari adalah setengah dari diameter alas kerucut.
2. Hitung panjang garis pelukis (s): Jika tinggi kerucut ($ t $) diketahui, gunakan teorema Pythagoras untuk menghitung $ s $:
   $$
   s = \sqrt{r^2 + t^2}
   $$
3. Gunakan rumus luas selimut: Setelah mendapatkan $ r $ dan $ s $, substitusi ke dalam rumus $ L = \pi \times r \times s $.

Contoh Soal Menghitung Luas Selimut Kerucut

Contoh Soal 1:

Sebuah kerucut memiliki jari-jari 7 cm dan tinggi 24 cm. Hitunglah luas selimut kerucut tersebut!

Langkah-langkah penyelesaian:
1. Cari panjang garis pelukis ($ s $):
$$
s = \sqrt{r^2 + t^2} = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25 \text{ cm}
$$
2. Hitung luas selimut:
$$
L = \pi \times r \times s = \frac{22}{7} \times 7 \times 25 = 22 \times 25 = 550 \text{ cm}^2
$$

Jawaban: Luas selimut kerucut adalah 550 cm².

Contoh Soal 2:

Sebuah kerucut memiliki diameter 14 cm dan garis pelukis 15 cm. Hitung luas selimut kerucut tersebut!

Langkah-langkah penyelesaian:
1. Hitung jari-jari:
$$
r = \frac{d}{2} = \frac{14}{2} = 7 \text{ cm}
$$
2. Hitung luas selimut:
$$
L = \pi \times r \times s = \frac{22}{7} \times 7 \times 15 = 22 \times 15 = 330 \text{ cm}^2
$$

Jawaban: Luas selimut kerucut adalah 330 cm².

Perbedaan Antara Luas Selimut dan Luas Permukaan Kerucut

Meskipun sering disamakan, luas selimut kerucut dan luas permukaan kerucut memiliki perbedaan yang signifikan:

• Luas selimut kerucut hanya menghitung area dari sisi melengkung saja.
• Luas permukaan kerucut mencakup seluruh permukaan, termasuk alas dan selimut.

Rumus luas permukaan kerucut adalah:
$$
L_{\text{permukaan}} = \pi \times r \times (r + s)
$$

Penerapan Rumus Luas Selimut Kerucut dalam Kehidupan Nyata

Rumus luas selimut kerucut tidak hanya digunakan dalam pelajaran matematika, tetapi juga dalam berbagai situasi nyata. Berikut beberapa contoh penerapan:

1. Membuat Topi Kerucut: Saat membuat topi kerucut dari kertas, kamu perlu mengetahui luas selimut agar bisa menentukan jumlah kertas yang dibutuhkan.
2. Desain Bangunan: Arsitek sering menggunakan kerucut dalam desain atap atau struktur tertentu, sehingga perhitungan luas selimut menjadi penting.
3. Industri Manufaktur: Dalam industri, perhitungan luas selimut kerucut digunakan untuk menentukan ukuran bahan baku yang diperlukan.

Tips dan Trik dalam Menghitung Luas Selimut Kerucut

1. Gunakan Pi yang Tepat: Jika diameter atau jari-jari adalah bilangan bulat yang habis dibagi 7, gunakan $ \frac{22}{7} $. Jika bukan, gunakan 3,14.
2. Periksa Satuan: Pastikan semua satuan (misalnya cm, m) konsisten.
3. Cari Garis Pelukis Terlebih Dahulu: Jika hanya diketahui tinggi dan jari-jari, gunakan teorema Pythagoras untuk mencari panjang garis pelukis.
4. Latihan Soal Berkala: Semakin banyak latihan, semakin mudah kamu menguasai rumus dan konsepnya.

Kesimpulan

Rumus luas selimut kerucut adalah salah satu konsep penting dalam geometri yang memiliki banyak penerapan dalam kehidupan nyata. Dengan memahami rumus $ L = \pi \times r \times s $ dan cara menghitungnya, kamu bisa menyelesaikan berbagai soal terkait kerucut dengan mudah. Selain itu, penguasaan konsep ini juga akan membantu kamu dalam memahami luas permukaan kerucut dan berbagai bentuk bangun ruang lainnya.

Dengan latihan dan pemahaman yang cukup, kamu pasti akan mampu menguasai rumus luas selimut kerucut dan menggunakannya dalam berbagai situasi. Jadi, jangan ragu untuk terus belajar dan berlatih!