Diagonal ruang balok adalah salah satu konsep penting dalam geometri yang sering muncul dalam berbagai soal matematika, terutama pada materi dimensi tiga. Dalam kehidupan sehari-hari, pemahaman tentang diagonal ruang balok juga berguna untuk menghitung jarak antara dua titik sudut yang saling berhadapan di dalam bangun ruang. Misalnya, ketika merancang struktur bangunan atau menghitung ukuran kemasan kotak, pengetahuan ini sangat bermanfaat.
Balok adalah bangun ruang tiga dimensi yang terdiri dari tiga pasang sisi persegi panjang atau persegi. Setiap balok memiliki 12 rusuk, 8 titik sudut, dan 6 bidang. Salah satu ciri khas balok adalah adanya diagonal ruang yang menghubungkan dua titik sudut yang tidak berada pada satu bidang. Diagonal ruang ini memainkan peran penting dalam menentukan dimensi ruang dalam balok.
Dalam artikel ini, kita akan membahas secara lengkap cara menghitung diagonal ruang balok. Kami akan menjelaskan definisinya, rumus yang digunakan, serta contoh soal yang mudah dipahami. Selain itu, kami juga akan memberikan tips dan trik agar kamu bisa menghitung diagonal ruang balok dengan cepat dan akurat. Jika kamu sedang belajar matematika atau ingin memperdalam pemahamanmu tentang geometri, artikel ini cocok untuk kamu baca.
Apa Itu Diagonal Ruang Balok?
Diagonal ruang balok adalah garis lurus yang menghubungkan dua titik sudut yang tidak berada pada satu bidang yang sama. Dalam sebuah balok, setiap titik sudut dapat dihubungkan dengan titik sudut lainnya melalui diagonal ruang. Karena balok memiliki 8 titik sudut, maka terdapat 4 diagonal ruang yang masing-masing memiliki panjang yang sama.
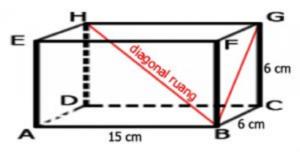
Contohnya, jika kamu melihat gambar balok ABCD.EFGH, diagonal ruangnya adalah AE, BF, CG, dan DH. Keempat diagonal ini menghubungkan titik-titik sudut yang berlawanan di dalam balok.
Penting untuk diketahui bahwa diagonal ruang berbeda dengan diagonal bidang. Diagonal bidang hanya menghubungkan dua titik sudut yang terletak pada satu bidang, sedangkan diagonal ruang melintasi seluruh volume balok.
Rumus Menghitung Diagonal Ruang Balok
Untuk menghitung panjang diagonal ruang balok, kita bisa menggunakan rumus berikut:
$$
\text{Panjang Diagonal Ruang} = \sqrt{p^2 + l^2 + t^2}
$$
Keterangan:
– $ p $ = panjang balok
– $ l $ = lebar balok
– $ t $ = tinggi balok
Rumus ini berasal dari teorema Pythagoras yang diperluas untuk tiga dimensi. Dengan menggabungkan panjang, lebar, dan tinggi balok, kita bisa menemukan jarak antara dua titik sudut yang berlawanan.
Sebagai contoh, jika sebuah balok memiliki panjang 4 cm, lebar 3 cm, dan tinggi 5 cm, maka panjang diagonal ruangnya adalah:
$$
\sqrt{4^2 + 3^2 + 5^2} = \sqrt{16 + 9 + 25} = \sqrt{50} \approx 7,07 \text{ cm}
$$
Dengan demikian, panjang diagonal ruang balok tersebut adalah sekitar 7,07 sentimeter.
Langkah-Langkah Menghitung Diagonal Ruang Balok
Berikut adalah langkah-langkah sistematis untuk menghitung diagonal ruang balok:
-
Identifikasi Panjang, Lebar, dan Tinggi Balok
Pastikan kamu mengetahui nilai dari panjang (p), lebar (l), dan tinggi (t) balok. Nilai-nilai ini biasanya diberikan dalam soal atau bisa diukur langsung dari objek yang diberikan. -
Kuadratkan Masing-Masing Dimensi
Hitung kuadrat dari panjang, lebar, dan tinggi balok. Contohnya: - $ p^2 $
- $ l^2 $
-
$ t^2 $
-
Jumlahkan Kuadrat Ketiga Dimensi
Tambahkan hasil kuadrat dari panjang, lebar, dan tinggi:
$$
p^2 + l^2 + t^2
$$ -
Hitung Akar Kuadrat dari Hasil Penjumlahan
Gunakan kalkulator atau hitung manual untuk mencari akar kuadrat dari jumlah yang telah kamu dapatkan. Hasilnya adalah panjang diagonal ruang balok. -
Tulis Jawaban dengan Satuan yang Sesuai
Pastikan jawaban disertai dengan satuan seperti sentimeter (cm) atau meter (m), sesuai dengan satuan yang digunakan dalam soal.
Contoh Soal dan Pembahasan
Contoh 1:
Sebuah balok memiliki panjang 6 cm, lebar 8 cm, dan tinggi 10 cm. Hitunglah panjang diagonal ruang balok tersebut!
Penyelesaian:
Gunakan rumus:
$$
\text{Diagonal Ruang} = \sqrt{p^2 + l^2 + t^2}
$$
Substitusi nilai:
$$
\text{Diagonal Ruang} = \sqrt{6^2 + 8^2 + 10^2} = \sqrt{36 + 64 + 100} = \sqrt{200} \approx 14,14 \text{ cm}
$$
Contoh 2:
Jika panjang balok adalah 5 cm, lebar 12 cm, dan tinggi 13 cm, berapa panjang diagonal ruangnya?
Penyelesaian:
$$
\text{Diagonal Ruang} = \sqrt{5^2 + 12^2 + 13^2} = \sqrt{25 + 144 + 169} = \sqrt{338} \approx 18,38 \text{ cm}
$$
Contoh 3:
Sebuah kotak berbentuk balok memiliki ukuran panjang 10 cm, lebar 24 cm, dan tinggi 26 cm. Hitunglah panjang diagonal ruangnya!
Penyelesaian:
$$
\text{Diagonal Ruang} = \sqrt{10^2 + 24^2 + 26^2} = \sqrt{100 + 576 + 676} = \sqrt{1352} \approx 36,77 \text{ cm}
$$
Tips dan Trik Menghitung Diagonal Ruang Balok
-
Gunakan Kalkulator untuk Akar Kuadrat
Jika kamu kesulitan menghitung akar kuadrat secara manual, gunakan kalkulator atau aplikasi matematika untuk mempercepat proses perhitungan. -
Periksa Kembali Nilai yang Digunakan
Pastikan kamu menggunakan nilai panjang, lebar, dan tinggi yang benar. Kesalahan dalam pengambilan data bisa menyebabkan hasil yang salah. -
Latihan dengan Berbagai Contoh Soal
Semakin banyak latihan, semakin mahir kamu dalam menghitung diagonal ruang balok. Coba kerjakan soal-soal dari buku pelajaran atau situs web edukasi. -
Coba Menggunakan Metode Visualisasi
Gambar atau visualisasi balok bisa membantu kamu lebih memahami bagaimana diagonal ruang bekerja. Kamu bisa membuat sketsa sederhana untuk mempermudah pemahaman.
Manfaat Memahami Diagonal Ruang Balok
Pemahaman tentang diagonal ruang balok tidak hanya berguna dalam ujian matematika, tetapi juga dalam berbagai situasi nyata. Berikut beberapa manfaatnya:
-
Desain Bangunan dan Arsitektur
Arsitek dan insinyur sering menggunakan konsep diagonal ruang untuk menghitung dimensi ruang dan memastikan struktur bangunan stabil. -
Pengemasan dan Logistik
Dalam industri pengemasan, diagonal ruang digunakan untuk menentukan ukuran kemasan yang optimal agar barang bisa masuk ke dalam wadah tanpa terganggu. -
Pembelajaran Matematika
Di sekolah, konsep ini diajarkan sebagai bagian dari geometri tiga dimensi, membantu siswa memahami hubungan antara bentuk dan ukuran. -
Penggunaan dalam Teknologi
Dalam dunia komputer grafis dan animasi, diagonal ruang digunakan untuk menghitung jarak antara titik-titik dalam ruang 3D.
Kesimpulan
Diagonal ruang balok adalah garis yang menghubungkan dua titik sudut yang tidak berada pada satu bidang yang sama. Untuk menghitungnya, kita menggunakan rumus:
$$
\text{Diagonal Ruang} = \sqrt{p^2 + l^2 + t^2}
$$
Dengan memahami konsep ini, kamu bisa menyelesaikan berbagai soal matematika yang berkaitan dengan balok. Selain itu, pemahaman ini juga berguna dalam kehidupan nyata, terutama dalam desain, logistik, dan teknologi. Dengan latihan yang cukup, kamu akan mampu menghitung diagonal ruang balok dengan cepat dan akurat.



















Komentar