Matematika sering kali dianggap sebagai pelajaran yang menantang, terutama bagi siswa yang sedang belajar. Namun, jika dilihat dari sudut pandang yang tepat, matematika justru menjadi fondasi penting untuk memahami berbagai konsep dalam kehidupan sehari-hari. Salah satu hal kunci yang membuat matematika lebih mudah dipahami adalah penguasaan rumus-rumus dasar dan lanjutan. Rumus matematika (rumus rumus mtk) tidak hanya membantu dalam menyelesaikan soal, tetapi juga meningkatkan kemampuan berpikir logis dan analitis. Dalam artikel ini, kita akan membahas kumpulan rumus matematika yang wajib diketahui oleh siswa, mulai dari bangun datar hingga konsep aljabar, trigonometri, dan statistik.
Rumus matematika adalah persamaan atau hubungan simbolik yang digunakan untuk menyelesaikan masalah. Ibarat alat tukang, rumus membantu kita mengukur, menghitung, membandingkan, dan memprediksi. Menguasai rumus bukan hanya tentang menghafal, tetapi juga memahami cara penggunaannya dalam berbagai situasi. Misalnya, rumus luas persegi atau lingkaran bisa digunakan dalam banyak kasus, baik dalam ujian maupun dalam kehidupan nyata. Oleh karena itu, pemahaman yang mendalam tentang rumus matematika sangat penting untuk meningkatkan keterampilan akademik dan daya pikir.
Selain itu, rumus matematika juga memiliki peran besar dalam berbagai bidang ilmu lain, seperti fisika, ekonomi, dan bahkan coding. Banyak ilmuwan dan ahli teknologi yang menggunakan rumus matematika sebagai dasar dalam penelitian dan pengembangan. Dengan memahami rumus matematika, siswa tidak hanya siap menghadapi ujian, tetapi juga memiliki bekal untuk menghadapi tantangan dunia nyata. Artikel ini akan memberikan panduan lengkap tentang rumus-rumus matematika yang harus dikuasai oleh siswa, beserta contoh dan penjelasan singkat agar lebih mudah dipahami.
Kumpulan Rumus Matematika Dasar
Berikut adalah beberapa rumus matematika dasar yang wajib diketahui oleh siswa:
- Rumus Perkalian dan Pembagian
- Perkalian: $ a \times b = b \times a $
-
Pembagian: $ \frac{a}{b} = c \Rightarrow a = b \times c $
-
Rumus Bangun Datar
- Luas Persegi: $ L = s \times s $
- Luas Segitiga: $ L = \frac{1}{2} \times a \times t $
- Luas Lingkaran: $ L = \pi r^2 $
-
Keliling Lingkaran: $ K = 2\pi r $
-
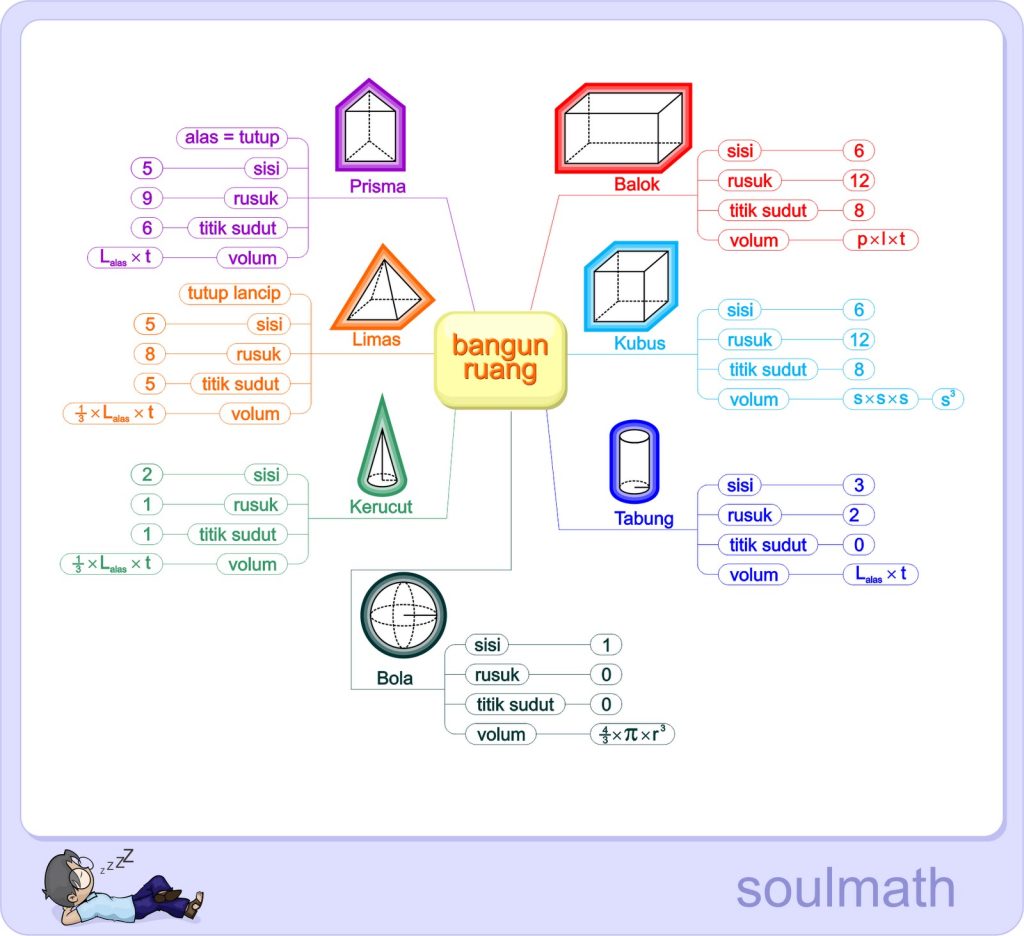
Rumus Bangun Ruang
- Volume Kubus: $ V = s^3 $
- Volume Balok: $ V = p \times l \times t $
-
Volume Tabung: $ V = \pi r^2 t $
-
Rumus Aritmetika
- Deret aritmetika: $ U_n = a + (n-1) \times b $
-
Jumlah n suku: $ S_n = \frac{n}{2} \times (2a + (n-1)b) $
-
Rumus Geometri
- Deret geometri: $ U_n = a \times r^{n-1} $
- Jumlah n suku: $ S_n = a \times \frac{r^n – 1}{r – 1} $ (untuk $ r \neq 1 $)
Rumus-rumus di atas merupakan fondasi dasar dalam matematika yang sering digunakan dalam berbagai topik pembelajaran. Dengan memahami dan menguasai rumus-rumus ini, siswa akan lebih mudah dalam menyelesaikan soal-soal matematika yang kompleks.
Rumus Matematika SMA: Aljabar, Trigonometri, Kalkulus, dan Statistik
Di tingkat SMA, siswa akan belajar berbagai konsep matematika yang lebih kompleks. Berikut adalah beberapa rumus penting yang sering digunakan:
Aljabar
- Pemfaktoran: $ ax^2 + bx + c = (x – x_1)(x – x_2) $
- Persamaan kuadrat: $ x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} $
Trigonometri
- Identitas dasar: $ \sin^2 x + \cos^2 x = 1 $
- Tangen: $ \tan x = \frac{\sin x}{\cos x} $
- Sudut rangkap: $ \sin 2x = 2 \sin x \cos x $
Kalkulus
- Turunan dasar: $ \frac{d}{dx} x^n = nx^{n-1} $
- Integral dasar: $ \int x^n dx = \frac{x^{n+1}}{n+1} + C $
Statistik
- Mean: $ \bar{x} = \frac{\sum x}{n} $
- Median: Data tengah setelah diurutkan
- Modus: Data yang paling sering muncul
Pemahaman tentang rumus-rumus ini sangat penting untuk menjawab soal-soal matematika tingkat lanjut. Selain itu, rumus-rumus ini juga menjadi dasar dalam berbagai bidang studi seperti sains, teknik, dan ekonomi.
Rumus yang Berisi Beberapa Operator Matematika Disebut Ekspresi Matematika
Dalam matematika, gabungan dari berbagai operator seperti tambah, kurang, kali, bagi, pangkat, dan kurung disebut sebagai ekspresi matematika. Contohnya, ekspresi $ 3 \times 2 + 5x – 2 $ mengandung beberapa operasi matematika yang harus diselesaikan dengan urutan tertentu.
Aturan penyelesaian ekspresi matematika disebut PEMDAS, yang merupakan singkatan dari:
– Parentheses (tanda kurung)
– Exponents (pangkat)
– Multiplication (perkalian)
– Division (pembagian)
– Addition (penjumlahan)
– Subtraction (pengurangan)
Dengan memahami aturan ini, siswa dapat menyelesaikan ekspresi matematika secara lebih efisien dan akurat.
Cara Menulis Rumus Matematika di Word dengan Mudah dan Rapi
Menulis rumus matematika di Word bisa dilakukan dengan fitur “Equation” yang tersedia di Microsoft Word. Berikut langkah-langkahnya:
- Tekan tombol Alt + = pada keyboard untuk membuka kotak equation.
- Ketik rumus menggunakan simbol atau LaTeX (jika aktif).
- Gunakan menu Insert > Equation untuk mengakses simbol-simbol matematika yang lebih lengkap.
Beberapa shortcut yang berguna:
– Kuadrat: x^2
– Pecahan: \frac{a}{b}
– Akar: \sqrt{x}
Word versi terbaru semakin mendukung penulisan rumus matematika, bahkan kamu bisa menulis dengan tangan di layar sentuh dan langsung diubah menjadi teks!
Siapa Penemu Rumus Matematika? Jejak Tokoh-Tokoh Penting dalam Sejarah
Banyak tokoh besar dalam sejarah matematika yang telah memberikan kontribusi besar dalam pengembangan rumus-rumus yang kita gunakan hari ini. Beberapa di antaranya adalah:
– Pythagoras: Penemu rumus segitiga siku-siku $ a^2 + b^2 = c^2 $
– Euclid: Bapak geometri; penulis buku “Elements”
– Isaac Newton & Leibniz: Pengembang kalkulus modern
– Carl Friedrich Gauss: Pakar teori bilangan dan statistik
– Blaise Pascal: Penemu segitiga Pascal dan teori probabilitas
Kisah-kisah mereka membuktikan bahwa matematika berkembang dari rasa penasaran dan logika yang kuat, bukan hanya dari jenius dari lahir.
Rumus Matematika yang Belum Terpecahkan dan Masih Jadi Misteri Dunia
Tidak semua rumus matematika memiliki jawaban. Masih banyak persoalan matematika yang belum terpecahkan, seperti:
– Hipotesis Riemann: Tentang distribusi bilangan prima
– P vs NP Problem: Menyangkut efisiensi algoritma komputer
– Collatz Conjecture: Teka-teki bilangan bulat sederhana
Beberapa soal ini bahkan termasuk dalam daftar 7 Millennium Prize Problems, dengan hadiah 1 juta dolar AS bagi siapa saja yang berhasil memecahkan salah satu dari soal tersebut. Ini menunjukkan bahwa matematika masih terus berkembang, dan mungkin saja kamu akan menjadi penemu rumus baru di masa depan.
Kesimpulan: Pahami Rumus, Pecahkan Soal, Kuasai Matematika
Rumus matematika adalah alat penting yang membantu kita menyelesaikan berbagai masalah. Dengan memahami dan menguasai rumus-rumus ini, siswa tidak hanya siap menghadapi ujian, tetapi juga memiliki bekal untuk menghadapi tantangan dunia nyata. Jadi, jangan hanya menghafal rumus, tetapi pahami cara kerjanya, latih dalam soal, dan carilah tahu kisah di baliknya. Siapa tahu, kamu bisa menjadi penemu rumus selanjutnya!



















Komentar