Dalam dunia matematika, istilah “rumus perpangkatan” sering muncul dalam berbagai topik seperti aljabar, geometri, dan bahkan fisika. Perpangkatan adalah salah satu konsep dasar yang sangat penting untuk memahami berbagai operasi matematika lebih lanjut. Dengan memahami rumus perpangkatan, kamu tidak hanya bisa menyelesaikan soal-soal matematika dengan lebih mudah, tetapi juga mengembangkan logika dan pemahaman tentang bagaimana bilangan-bilangan dapat dinyatakan dalam bentuk yang lebih sederhana dan efisien.
Rumus perpangkatan sendiri merujuk pada proses pengulangan perkalian suatu bilangan dengan dirinya sendiri sebanyak jumlah pangkat yang diberikan. Misalnya, 2³ berarti 2 × 2 × 2. Konsep ini sangat berguna dalam berbagai bidang, termasuk ilmu pengetahuan, teknologi, dan ekonomi. Selain itu, rumus perpangkatan juga menjadi dasar dari banyak teori matematika yang lebih kompleks, seperti fungsi eksponensial dan persamaan kuadrat.
Pemahaman yang baik terhadap rumus perpangkatan akan membantu kamu dalam menghadapi berbagai masalah matematika, baik dalam ujian sekolah maupun dalam kehidupan sehari-hari. Contohnya, dalam ilmu fisika, kecepatan cahaya sering dinyatakan dalam bentuk bilangan berpangkat untuk mempermudah penyajian dan perhitungan. Di bidang ekonomi, perhitungan bunga majemuk juga menggunakan konsep perpangkatan. Oleh karena itu, mempelajari rumus perpangkatan bukan hanya penting untuk belajar matematika, tetapi juga untuk memperluas wawasan dan keterampilan analitis.
Artikel ini akan membahas secara lengkap tentang rumus perpangkatan, mulai dari pengertian dasar hingga contoh soal dan penerapan praktisnya. Kami juga akan menjelaskan berbagai sifat-sifat bilangan berpangkat, serta cara menggunakannya dalam berbagai situasi. Dengan informasi yang disajikan, diharapkan pembaca dapat memahami dan menguasai konsep perpangkatan dengan lebih baik.
Pengertian Dasar Rumus Perpangkatan
Rumus perpangkatan adalah konsep matematika yang digunakan untuk menyatakan perkalian berulang dari suatu bilangan dengan dirinya sendiri. Bilangan tersebut disebut sebagai basis atau bilangan pokok, sedangkan angka yang menunjukkan seberapa banyak bilangan tersebut dikalikan disebut pangkat atau eksponen. Secara umum, rumus perpangkatan dapat ditulis dalam bentuk:
a^n = a × a × a × … × a (sebanyak n kali)
Di mana:
– a adalah basis (bilangan yang dipangkatkan)
– n adalah pangkat (jumlah pengulangan perkalian)
Contohnya, jika kita memiliki 3^4, maka artinya 3 dikalikan dengan dirinya sendiri sebanyak 4 kali, yaitu 3 × 3 × 3 × 3 = 81.
Perpangkatan ini sering digunakan dalam berbagai bidang, termasuk ilmu pengetahuan dan teknologi. Misalnya, dalam fisika, kecepatan cahaya biasanya dinyatakan dalam bentuk bilangan berpangkat, seperti 3 × 10^8 meter per detik. Dalam ekonomi, perhitungan bunga majemuk juga menggunakan konsep perpangkatan untuk menentukan nilai investasi di masa depan.
Selain itu, rumus perpangkatan juga digunakan dalam pengkodean data dan enkripsi, yang sangat penting dalam dunia digital saat ini. Dengan memahami konsep dasar ini, kamu akan lebih mudah menghadapi berbagai masalah matematika yang melibatkan bilangan berpangkat.
Jenis-Jenis Bilangan Berpangkat
Bilangan berpangkat dapat dibagi menjadi beberapa jenis berdasarkan tanda pangkatnya. Berikut ini adalah dua jenis utama dari bilangan berpangkat:
1. Bilangan Berpangkat Positif
Bilangan berpangkat positif adalah bilangan yang memiliki pangkat berupa bilangan bulat positif. Contoh dari bilangan berpangkat positif antara lain:
– 2^2 = 2 × 2 = 4
– 3^3 = 3 × 3 × 3 = 27
– 5^4 = 5 × 5 × 5 × 5 = 625
Semakin besar pangkatnya, semakin besar pula nilai bilangannya. Namun, ada juga kasus di mana pangkatnya kecil, namun hasilnya bisa sangat besar. Misalnya, 2^10 = 1024, yang merupakan bilangan yang cukup besar meskipun pangkatnya hanya 10.
2. Bilangan Berpangkat Negatif
Bilangan berpangkat negatif adalah bilangan yang memiliki pangkat berupa bilangan bulat negatif. Contoh dari bilangan berpangkat negatif antara lain:
– 2^-2 = 1/(2^2) = 1/4
– 3^-3 = 1/(3^3) = 1/27
– 5^-4 = 1/(5^4) = 1/625
Bilangan berpangkat negatif dapat diubah menjadi bentuk pecahan dengan membalik basisnya dan mengubah pangkatnya menjadi positif. Misalnya, 2^-2 = 1/(2^2), dan 3^-3 = 1/(3^3).
Selain itu, ada juga bilangan berpangkat nol, yang selalu bernilai 1, terlepas dari basisnya. Contohnya, 5^0 = 1, 10^0 = 1, dan 100^0 = 1. Ini adalah sifat khusus dari bilangan berpangkat yang sangat penting dalam berbagai perhitungan matematika.
Sifat-Sifat Bilangan Berpangkat
Bilangan berpangkat memiliki beberapa sifat yang sangat berguna dalam menyelesaikan berbagai masalah matematika. Berikut ini adalah sifat-sifat utama dari bilangan berpangkat:
1. Perkalian Bilangan Berpangkat dengan Basis Sama
Jika dua bilangan berpangkat memiliki basis yang sama, maka hasil perkaliannya adalah bilangan tersebut dengan pangkat yang dijumlahkan. Secara matematis, sifat ini dapat ditulis sebagai:
a^m × a^n = a^(m+n)
Contoh:
– 2^3 × 2^2 = 2^(3+2) = 2^5 = 32
– 5^4 × 5^1 = 5^(4+1) = 5^5 = 3125
2. Pembagian Bilangan Berpangkat dengan Basis Sama
Jika dua bilangan berpangkat memiliki basis yang sama, maka hasil pembagiannya adalah bilangan tersebut dengan pangkat yang dikurangi. Secara matematis, sifat ini dapat ditulis sebagai:
a^m ÷ a^n = a^(m-n)
Contoh:
– 2^5 ÷ 2^2 = 2^(5-2) = 2^3 = 8
– 5^6 ÷ 5^3 = 5^(6-3) = 5^3 = 125
3. Pangkat dari Bilangan Berpangkat
Jika suatu bilangan berpangkat dipangkatkan lagi, maka pangkatnya akan dikalikan. Secara matematis, sifat ini dapat ditulis sebagai:
(a^m)^n = a^(m×n)
Contoh:
– (2^3)^2 = 2^(3×2) = 2^6 = 64
– (5^2)^3 = 5^(2×3) = 5^6 = 15.625
4. Pangkat Nol
Setiap bilangan yang dipangkatkan nol akan selalu bernilai 1, asalkan basisnya bukan nol. Secara matematis, sifat ini dapat ditulis sebagai:
a^0 = 1 (dengan a ≠ 0)
Contoh:
– 5^0 = 1
– 10^0 = 1
– (-3)^0 = 1
5. Pangkat Negatif
Bilangan berpangkat negatif dapat diubah menjadi bentuk pecahan dengan membalik basisnya dan mengubah pangkatnya menjadi positif. Secara matematis, sifat ini dapat ditulis sebagai:
a^-n = 1/(a^n)
Contoh:
– 2^-2 = 1/(2^2) = 1/4
– 3^-3 = 1/(3^3) = 1/27
Contoh Soal dan Penyelesaian
Untuk lebih memahami konsep rumus perpangkatan, berikut ini adalah beberapa contoh soal beserta penyelesaiannya:
Contoh 1
Hitunglah nilai dari 3^4!
Penyelesaian:
3^4 = 3 × 3 × 3 × 3 = 81
Contoh 2
Hitunglah nilai dari 5^2 × 5^3!
Penyelesaian:
5^2 × 5^3 = 5^(2+3) = 5^5 = 3125
Contoh 3
Hitunglah nilai dari 2^5 ÷ 2^2!
Penyelesaian:
2^5 ÷ 2^2 = 2^(5-2) = 2^3 = 8
Contoh 4
Hitunglah nilai dari (4^2)^3!
Penyelesaian:
(4^2)^3 = 4^(2×3) = 4^6 = 4096
Contoh 5
Hitunglah nilai dari 10^0!
Penyelesaian:
10^0 = 1
Penerapan Rumus Perpangkatan dalam Kehidupan Sehari-Hari
Rumus perpangkatan tidak hanya digunakan dalam matematika, tetapi juga dalam berbagai situasi kehidupan sehari-hari. Berikut ini adalah beberapa contoh penerapan rumus perpangkatan:
1. Perhitungan Bunga Majemuk
Dalam dunia keuangan, perhitungan bunga majemuk menggunakan konsep perpangkatan untuk menentukan nilai investasi di masa depan. Rumus bunga majemuk adalah:
A = P(1 + r/n)^(nt)
Di mana:
– A = jumlah akhir
– P = pokok awal
– r = tingkat bunga
– n = frekuensi pembayaran bunga
– t = waktu
2. Ilmu Fisika
Dalam ilmu fisika, kecepatan cahaya sering dinyatakan dalam bentuk bilangan berpangkat. Misalnya, kecepatan cahaya adalah 3 × 10^8 meter per detik. Hal ini mempermudah penyajian dan perhitungan dalam berbagai aplikasi teknologi.
3. Pengkodean Data
Dalam dunia komputer dan teknologi informasi, pengkodean data sering menggunakan konsep perpangkatan untuk menyimpan dan mengenkripsi informasi. Contohnya, sistem biner menggunakan pangkat dua untuk merepresentasikan berbagai nilai.
4. Perhitungan Jumlah Penduduk
Dalam demografi, perhitungan pertumbuhan penduduk sering menggunakan model eksponensial, yang melibatkan konsep perpangkatan untuk memprediksi jumlah penduduk di masa depan.
Kesimpulan
Rumus perpangkatan adalah salah satu konsep dasar dalam matematika yang sangat penting. Dengan memahami rumus perpangkatan, kamu akan lebih mudah menyelesaikan berbagai masalah matematika, baik dalam ujian maupun dalam kehidupan sehari-hari. Dari pengertian dasar hingga contoh soal dan penerapan praktis, artikel ini telah memberikan panduan lengkap untuk memahami konsep perpangkatan.
Selain itu, kamu juga telah belajar tentang berbagai sifat bilangan berpangkat, seperti perkalian, pembagian, pangkat dari bilangan berpangkat, pangkat nol, dan pangkat negatif. Dengan memahami sifat-sifat ini, kamu akan lebih percaya diri dalam menghadapi berbagai masalah matematika yang melibatkan bilangan berpangkat.
Pemahaman yang baik tentang rumus perpangkatan juga akan membantu kamu dalam berbagai bidang, seperti ilmu pengetahuan, teknologi, dan ekonomi. Oleh karena itu, jangan ragu untuk terus berlatih dan menguasai konsep ini agar kamu bisa menggunakannya dengan optimal dalam berbagai situasi.



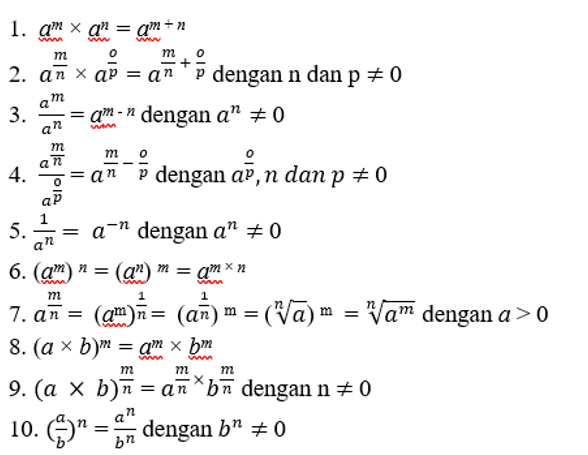
















Komentar