Pahami Metode Horner: Cara Sederhana Menghitung Nilai Polinomial

Dalam dunia matematika, metode Horner sering menjadi topik yang menarik untuk dipelajari, terutama ketika berbicara tentang evaluasi dan pembagian polinomial. Dikenal sebagai algoritma yang efisien, metode ini memungkinkan kita untuk menghitung nilai polinomial dengan cara yang lebih sederhana dibandingkan metode konvensional. Banyak siswa dan penggemar matematika mencari informasi tentang bagaimana metode ini bekerja dan bagaimana menerapkannya dalam berbagai situasi.

Metode Horner tidak hanya berguna dalam perhitungan matematis, tetapi juga memiliki aplikasi nyata dalam bidang teknologi dan ilmu komputer. Dengan menggunakan langkah-langkah yang sistematis dan logis, metode ini membantu mengurangi kompleksitas perhitungan, terutama ketika menangani polinomial berderajat tinggi. Selain itu, metode ini juga digunakan untuk mencari akar-akar dari suatu persamaan polinomial, yang merupakan hal penting dalam analisis matematika.

Ketertarikan terhadap metode Horner tidak hanya terbatas pada para pelajar, tetapi juga bagi para peneliti dan ahli matematika yang ingin memahami cara-cara modern dalam menyelesaikan masalah matematika. Artikel ini akan membahas secara mendalam tentang metode Horner, termasuk sejarahnya, cara kerjanya, serta contoh penerapan dalam soal-soal matematika. Dengan penjelasan yang jelas dan mudah dipahami, artikel ini bertujuan untuk memberikan pemahaman yang baik tentang metode Horner dan manfaatnya dalam kehidupan sehari-hari.

Sejarah dan Prinsip Dasar Metode Horner

Metode Horner ditemukan oleh William George Horner, seorang matematikawan Inggris pada abad ke-19. Namun, sejarah menunjukkan bahwa prinsip dasar dari metode ini telah diketahui oleh matematikawan Cina dan Persia ratusan tahun sebelumnya. Meskipun demikian, metode ini dinamai sesuai dengan nama Horner karena ia berhasil mempopulerkan dan menyempurnakan algoritma tersebut dalam konteks modern.

Prinsip dasar dari metode Horner adalah untuk mengubah bentuk polinomial agar dapat dievaluasi dengan lebih cepat dan efisien. Misalnya, jika kita memiliki polinomial seperti:

$$ f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + \dots + a_nx^n $$

Maka, dengan metode Horner, kita dapat menulis ulang polinomial tersebut dalam bentuk yang lebih sederhana, yaitu:

$$ f(x) = a_0 + x(a_1 + x(a_2 + x(a_3 + \dots + x(a_{n-1} + x a_n)\dots))) $$

Dengan cara ini, kita hanya membutuhkan sejumlah operasi perkalian dan penjumlahan yang sama dengan derajat polinomial. Ini membuat metode Horner sangat efisien, terutama ketika menghadapi polinomial berderajat tinggi.

Metode ini juga digunakan untuk mencari akar-akar dari suatu polinomial. Dengan mengganti nilai $ x $ tertentu, kita dapat mengetahui apakah nilai tersebut adalah akar dari polinomial tersebut. Hal ini sangat berguna dalam berbagai aplikasi matematika dan teknik.

Langkah-Langkah Penerapan Metode Horner

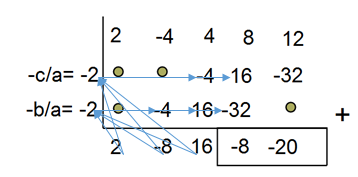
Untuk menerapkan metode Horner, kita perlu mengikuti beberapa langkah yang sistematis. Berikut adalah langkah-langkah umum dalam menggunakan metode Horner:

1. Tulis Koefisien Polinomial
   
   Mulailah dengan menuliskan semua koefisien dari polinomial yang diberikan. Misalnya, jika polinomialnya adalah $ f(x) = 5x^4 – 2x^3 + 3x^2 – 4x + 2 $, maka koefisiennya adalah 5, -2, 3, -4, dan 2.

2. Tentukan Nilai x yang Digunakan
   
   Jika kita ingin mengevaluasi polinomial pada nilai tertentu $ x $, maka kita perlu menentukan nilai tersebut. Misalnya, jika kita ingin mengevaluasi $ f(x) $ pada $ x = -2 $, maka nilai $ x $ yang digunakan adalah -2.

3. Mulai dengan Angka Pertama
   
   Kalikan angka pertama (koefisien terbesar) dengan nilai $ x $ yang telah ditentukan, lalu tambahkan hasilnya ke koefisien berikutnya.

4. Lanjutkan Proses Ini
   
   Ulangi langkah di atas untuk setiap koefisien berikutnya hingga mencapai akhir daftar koefisien.

   Read also: Ordinal and Cardinal Number Concept in Mathematics

5. Hasil Akhir
   
   Setelah menyelesaikan seluruh proses, hasil akhir akan memberikan nilai dari polinomial tersebut pada nilai $ x $ yang diberikan.

Contoh penerapan metode Horner dapat dilihat dalam soal-soal matematika, seperti yang disebutkan dalam referensi. Misalnya, ketika kita ingin menentukan hasil bagi dan sisa dari $ f(x) = 5x^4 – 2x^3 + 3x^2 – 4x + 2 $ dengan $ x + 2 $, kita dapat menggunakan metode Horner untuk menyelesaikannya secara efisien.

Keunggulan dan Manfaat Metode Horner

Metode Horner memiliki beberapa keunggulan yang membuatnya menjadi pilihan populer dalam berbagai situasi. Berikut adalah beberapa manfaat utama dari metode ini:

1. Efisiensi dalam Perhitungan
   
   Metode Horner hanya membutuhkan sejumlah operasi perkalian dan penjumlahan yang sama dengan derajat polinomial. Ini membuatnya lebih efisien dibandingkan metode konvensional yang memerlukan banyak langkah perhitungan.

2. Mengurangi Kesalahan Perhitungan
   
   Karena metode ini menggunakan langkah-langkah yang sistematis dan logis, risiko kesalahan perhitungan dapat diminimalkan. Hal ini terutama penting ketika menangani polinomial berderajat tinggi.

3. Mudah Dipahami dan Diterapkan
   
   Metode Horner tidak memerlukan pengetahuan matematika yang terlalu rumit. Dengan penjelasan yang jelas, siapa pun dapat memahami dan menerapkannya dalam berbagai situasi.

4. Aplikasi dalam Bidang Teknologi dan Ilmu Komputer
   
   Metode ini digunakan dalam berbagai bidang, termasuk ilmu komputer dan teknik. Contohnya, metode Horner digunakan dalam algoritma untuk evaluasi polinomial dalam komputasi numerik.

5. Membantu dalam Mencari Akar Polinomial
   
   Metode Horner juga digunakan untuk mencari akar-akar dari suatu polinomial. Dengan mengganti nilai $ x $ tertentu, kita dapat mengetahui apakah nilai tersebut adalah akar dari polinomial tersebut.

Contoh Soal dan Penerapan Metode Horner

Untuk memperjelas pemahaman tentang metode Horner, berikut adalah beberapa contoh soal beserta penyelesaiannya:

Contoh Soal 1:

Tentukan hasil bagi dan sisa dari $ f(x) = 2x^3 – 3x^2 + 4x – 5 $ dengan $ x – 2 $ menggunakan metode Horner.

Langkah Penyelesaian:
1. Koefisien: 2, -3, 4, -5
2. Nilai $ x $: 2
3. Hitung:
– 2 × 2 = 4 → -3 + 4 = 1
– 1 × 2 = 2 → 4 + 2 = 6
– 6 × 2 = 12 → -5 + 12 = 7
4. Hasil: $ 2x^2 + x + 2 $, sisa 7

Contoh Soal 2:

Bagaimana hasil bagi dan sisa dari $ f(x) = x^4 – 2x^3 + x^2 – x + 1 $ dengan $ x^2 – x + 1 $ menggunakan cara bersusun?

Langkah Penyelesaian:
1. Bagi $ x^4 – 2x^3 + x^2 – x + 1 $ dengan $ x^2 – x + 1 $
2. Hasil: $ x^2 – x + 1 $, sisa 1

Contoh Soal 3:

Temukan hasil bagi dan sisa dari $ f(x) = 3x^3 – x^2 + 5x – 7 $ dengan $ x + 1 $ menggunakan metode Horner.

Langkah Penyelesaian:
1. Koefisien: 3, -1, 5, -7
2. Nilai $ x $: -1
3. Hitung:
– 3 × -1 = -3 → -1 + (-3) = -4
– -4 × -1 = 4 → 5 + 4 = 9
– 9 × -1 = -9 → -7 + (-9) = -16
4. Hasil: $ 3x^2 – 4x + 9 $, sisa -16

Tips dan Trik dalam Menggunakan Metode Horner

Meskipun metode Horner terlihat sederhana, ada beberapa tips dan trik yang bisa membantu Anda menggunakannya secara efektif:

1. Periksa Koefisien dengan Teliti
   
   Pastikan semua koefisien dari polinomial yang diberikan sudah benar dan lengkap. Kesalahan dalam menulis koefisien bisa menyebabkan hasil yang salah.

2. Gunakan Tabel untuk Mempermudah Perhitungan
   
   Jika Anda merasa bingung dengan langkah-langkahnya, gunakan tabel untuk mencatat setiap tahap perhitungan. Hal ini akan membantu Anda melacak setiap langkah dengan lebih jelas.

3. Latihan Secara Berkala
   
   Seperti halnya keterampilan lainnya, kemampuan dalam menggunakan metode Horner membutuhkan latihan yang cukup. Latih diri Anda dengan berbagai jenis soal agar semakin mahir.

4. Pahami Konsep Dasar Matematika
   
   Meskipun metode Horner tidak terlalu rumit, pemahaman dasar tentang polinomial dan operasi matematika akan sangat membantu dalam menerapkannya.

5. Gunakan Alat Bantu Digital
   
   Jika memungkinkan, gunakan alat bantu digital seperti kalkulator atau software matematika untuk memverifikasi hasil perhitungan Anda. Ini bisa menjadi cara yang efektif untuk memastikan keakuratan.

Kesimpulan

Metode Horner adalah algoritma yang sangat efisien dalam evaluasi dan pembagian polinomial. Dengan langkah-langkah yang sistematis dan logis, metode ini membantu mengurangi kompleksitas perhitungan, terutama ketika menangani polinomial berderajat tinggi. Selain itu, metode ini juga digunakan dalam mencari akar-akar dari suatu polinomial, yang merupakan hal penting dalam berbagai bidang.

Artikel ini telah menjelaskan sejarah, prinsip dasar, langkah-langkah penerapan, keunggulan, dan contoh soal yang dapat membantu Anda memahami metode Horner secara lebih mendalam. Dengan latihan yang cukup dan pemahaman yang baik, siapa pun dapat menguasai teknik ini dan menerapkannya dalam berbagai situasi matematika.

Jika Anda tertarik untuk belajar lebih lanjut tentang metode Horner atau ingin berlatih dengan soal-soal tambahan, jangan ragu untuk mencari sumber-sumber tambahan seperti buku teks, situs web, atau forum diskusi matematika. Semangat belajar dan semoga artikel ini bermanfaat bagi Anda!