Refleksi adalah salah satu konsep penting dalam geometri yang sering digunakan untuk memahami bagaimana objek berubah posisinya ketika dipantulkan oleh suatu permukaan datar. Dalam konteks matematika, refleksi didefinisikan sebagai transformasi yang memindahkan setiap titik pada bidang dengan menggunakan sifat bayangan cermin dari titik tersebut. Proses ini sangat relevan dalam berbagai bidang seperti seni, fisika, dan teknik. Dengan memahami rumus refleksi, kita dapat menghitung dan memprediksi perubahan posisi suatu objek secara akurat.
Pemahaman tentang refleksi tidak hanya berguna dalam studi matematika, tetapi juga dalam kehidupan sehari-hari. Misalnya, saat kita bercermin, kita melihat bayangan diri kita yang terlihat sama persis, namun posisinya berlawanan. Hal ini merupakan contoh nyata dari refleksi. Di sekolah, siswa seringkali belajar tentang refleksi sebagai bagian dari materi geometri, khususnya dalam bab transformasi geometri. Oleh karena itu, pemahaman mendalam tentang rumus refleksi sangat penting untuk memperkuat dasar matematika.
Artikel ini akan membahas secara rinci tentang rumus refleksi dalam matematika, termasuk berbagai jenis refleksi seperti refleksi terhadap sumbu-x, sumbu-y, titik asal, garis y = x, garis y = -x, serta garis vertikal dan horizontal. Selain itu, artikel ini juga akan menyertakan contoh soal dan penjelasan langkah demi langkah agar pembaca dapat memahami dan menerapkan konsep ini secara efektif.
Pengertian Refleksi dalam Matematika
Refleksi dalam matematika adalah transformasi geometri yang memindahkan setiap titik pada bidang dengan menggunakan sifat bayangan cermin dari titik tersebut. Dalam istilah sederhana, refleksi adalah proses memantulkan suatu objek terhadap suatu garis atau titik tertentu, sehingga menghasilkan bayangan yang memiliki bentuk dan ukuran yang sama dengan objek aslinya, tetapi posisinya berlawanan.
Sifat utama dari refleksi adalah bahwa jarak antara titik asal dan cermin (garis atau titik) sama dengan jarak antara titik bayangan dan cermin. Selain itu, garis yang menghubungkan titik asal dan titik bayangan selalu tegak lurus terhadap cermin. Hal ini menunjukkan bahwa refleksi tidak mengubah bentuk atau ukuran objek, hanya mengubah posisi dan orientasinya.
Dalam matematika, refleksi biasanya dilambangkan dengan huruf M. Contohnya, jika titik P(x, y) mengalami refleksi, maka hasilnya adalah titik P’(x’, y’). Secara matematis, ini dapat dinyatakan sebagai:
$$
M(P) = P’
$$
Refleksi juga memiliki beberapa sifat khusus, seperti:
- Jarak titik asal ke cermin sama dengan jarak titik bayangan ke cermin.
- Garis penghubung antara titik asal dan titik bayangan tegak lurus terhadap cermin.
- Semua garis penghubung antara titik asal dan titik bayangan saling sejajar.
- Pusat refleksi bisa dianggap sebagai cermin.
Dengan memahami sifat-sifat ini, kita dapat lebih mudah memahami bagaimana refleksi bekerja dan menerapkannya dalam berbagai situasi.
Jenis-Jenis Refleksi dalam Matematika
Dalam matematika, refleksi dibagi menjadi beberapa jenis berdasarkan sumbu atau garis yang digunakan sebagai cermin. Berikut adalah beberapa jenis refleksi yang umum ditemukan:
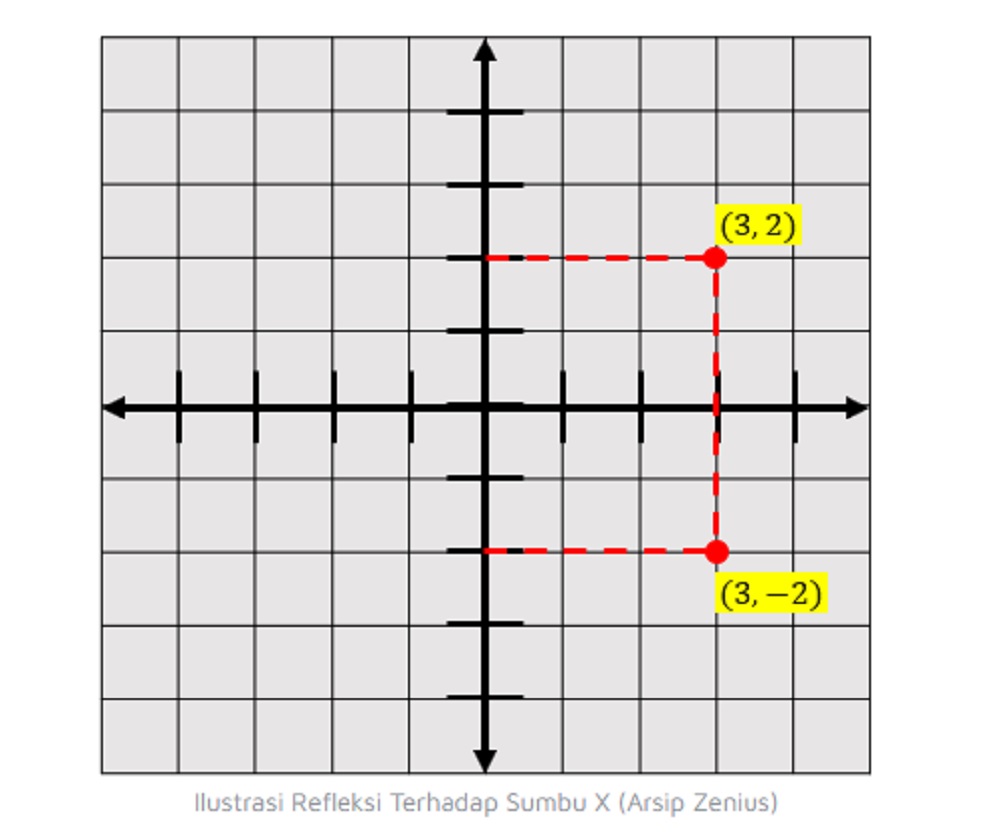
1. Refleksi terhadap Sumbu X
Refleksi terhadap sumbu X adalah transformasi yang memantulkan suatu titik terhadap garis horizontal (sumbu X). Dalam hal ini, koordinat y dari titik akan berubah tanda, sedangkan koordinat x tetap sama. Secara matematis, jika titik P(x, y) direfleksikan terhadap sumbu X, maka hasilnya adalah titik P’(x, -y).
Contoh:
Jika titik A(2, 3) direfleksikan terhadap sumbu X, maka bayangannya adalah A'(2, -3).
2. Refleksi terhadap Sumbu Y
Refleksi terhadap sumbu Y adalah transformasi yang memantulkan suatu titik terhadap garis vertikal (sumbu Y). Dalam hal ini, koordinat x dari titik akan berubah tanda, sedangkan koordinat y tetap sama. Secara matematis, jika titik P(x, y) direfleksikan terhadap sumbu Y, maka hasilnya adalah titik P’(-x, y).
Contoh:
Jika titik B(4, 5) direfleksikan terhadap sumbu Y, maka bayangannya adalah B'(-4, 5).
3. Refleksi terhadap Titik Asal (0, 0)
Refleksi terhadap titik asal adalah transformasi yang memantulkan suatu titik terhadap titik pusat (0, 0). Dalam hal ini, baik koordinat x maupun y dari titik akan berubah tanda. Secara matematis, jika titik P(x, y) direfleksikan terhadap titik asal, maka hasilnya adalah titik P’(-x, -y).
Contoh:
Jika titik C(3, -2) direfleksikan terhadap titik asal, maka bayangannya adalah C'(-3, 2).
4. Refleksi terhadap Garis y = x
Refleksi terhadap garis y = x adalah transformasi yang memantulkan suatu titik terhadap garis diagonal. Dalam hal ini, koordinat x dan y dari titik akan bertukar tempat. Secara matematis, jika titik P(x, y) direfleksikan terhadap garis y = x, maka hasilnya adalah titik P’(y, x).
Contoh:
Jika titik D(1, 4) direfleksikan terhadap garis y = x, maka bayangannya adalah D'(4, 1).
5. Refleksi terhadap Garis y = -x
Refleksi terhadap garis y = -x adalah transformasi yang memantulkan suatu titik terhadap garis diagonal lainnya. Dalam hal ini, koordinat x dan y dari titik akan bertukar tempat dan keduanya berubah tanda. Secara matematis, jika titik P(x, y) direfleksikan terhadap garis y = -x, maka hasilnya adalah titik P’(-y, -x).
Contoh:
Jika titik E(2, -3) direfleksikan terhadap garis y = -x, maka bayangannya adalah E'(3, -2).
6. Refleksi terhadap Garis x = h
Refleksi terhadap garis x = h adalah transformasi yang memantulkan suatu titik terhadap garis vertikal x = h. Dalam hal ini, koordinat x dari titik akan dihitung dengan rumus 2h – x, sedangkan koordinat y tetap sama. Secara matematis, jika titik P(x, y) direfleksikan terhadap garis x = h, maka hasilnya adalah titik P’(2h – x, y).
Contoh:
Jika titik F(1, 5) direfleksikan terhadap garis x = 3, maka bayangannya adalah F'(5, 5).
7. Refleksi terhadap Garis y = k
Refleksi terhadap garis y = k adalah transformasi yang memantulkan suatu titik terhadap garis horizontal y = k. Dalam hal ini, koordinat y dari titik akan dihitung dengan rumus 2k – y, sedangkan koordinat x tetap sama. Secara matematis, jika titik P(x, y) direfleksikan terhadap garis y = k, maka hasilnya adalah titik P’(x, 2k – y).
Contoh:
Jika titik G(2, 1) direfleksikan terhadap garis y = 4, maka bayangannya adalah G'(2, 7).
Dengan memahami jenis-jenis refleksi ini, kita dapat lebih mudah mengidentifikasi dan menerapkan konsep refleksi dalam berbagai situasi matematika.
Contoh Soal dan Penjelasan Rumus Refleksi
Untuk memperdalam pemahaman tentang rumus refleksi, berikut ini beberapa contoh soal beserta penjelasannya:
Contoh Soal 1
Tentukan bayangan dari titik A(6, -3) oleh pencerminan terhadap sumbu X.
Penyelesaian:
Dalam refleksi terhadap sumbu X, koordinat y dari titik akan berubah tanda, sedangkan koordinat x tetap sama. Jadi, jika titik A(6, -3) direfleksikan terhadap sumbu X, maka bayangannya adalah A'(6, 3).
Contoh Soal 2
Tentukan bayangan dari segitiga dengan titik S(-2, 4), T(3, -7), dan U(6, 5) oleh pencerminan terhadap sumbu y = -x.
Penyelesaian:
Dalam refleksi terhadap garis y = -x, koordinat x dan y dari titik akan bertukar tempat dan keduanya berubah tanda. Jadi, bayangan dari titik S(-2, 4) adalah S'(4, 2), bayangan dari titik T(3, -7) adalah T'(7, -3), dan bayangan dari titik U(6, 5) adalah U'(-5, -6).
Contoh Soal 3
Tentukan bayangan dari garis y = -x + 3 jika dicerminkan terhadap garis y = -x.
Penyelesaian:
Dalam refleksi terhadap garis y = -x, koordinat x dan y dari titik akan bertukar tempat dan keduanya berubah tanda. Dengan substitusi, kita dapat menemukan bahwa persamaan garis bayangannya adalah y = x – 3.
Contoh Soal 4
Tentukan bayangan dari titik (-4, 1) oleh pencerminan terhadap garis x = h, sehingga dihasilkan bayangan (-20, 1).
Penyelesaian:
Dalam refleksi terhadap garis x = h, koordinat x dari titik akan dihitung dengan rumus 2h – x. Dengan menggunakan rumus tersebut, kita dapat menentukan bahwa nilai h adalah -12.
Contoh Soal 5
Tentukan koordinat bayangan dari titik (-3, -1) oleh pencerminan terhadap garis y = -2.
Penyelesaian:
Dalam refleksi terhadap garis y = -2, koordinat y dari titik akan dihitung dengan rumus 2k – y. Dengan menggunakan rumus tersebut, kita dapat menentukan bahwa koordinat bayangan dari titik tersebut adalah (-3, -3).
Dengan mengerjakan contoh soal-soal ini, kita dapat lebih memahami cara menerapkan rumus refleksi dalam berbagai situasi. Ini juga membantu meningkatkan kemampuan analitis dan logika dalam menyelesaikan masalah matematika terkait refleksi.
Penerapan Rumus Refleksi dalam Kehidupan Sehari-Hari
Rumus refleksi tidak hanya digunakan dalam studi matematika, tetapi juga memiliki penerapan nyata dalam kehidupan sehari-hari. Salah satu contoh paling umum adalah saat kita bercermin. Bayangan yang kita lihat di cermin merupakan hasil dari refleksi yang terjadi pada permukaan datar. Dalam kasus ini, jarak antara wajah kita dengan cermin sama dengan jarak antara bayangan kita dengan cermin, dan posisi bayangan berlawanan dengan posisi aslinya.
Selain itu, refleksi juga digunakan dalam berbagai bidang seperti seni, desain grafis, dan teknik. Dalam seni, para seniman sering menggunakan prinsip refleksi untuk menciptakan karya yang simetris dan estetis. Dalam desain grafis, refleksi digunakan untuk membuat efek visual yang menarik dan menyeimbangkan komposisi gambar. Dalam teknik, refleksi digunakan untuk menghitung dan merancang struktur yang memerlukan simetri dan keseimbangan.
Dalam bidang fisika, refleksi juga menjadi dasar dari banyak fenomena alam, seperti pantulan cahaya dan suara. Contohnya, saat cahaya mengenai permukaan datar, ia akan dipantulkan sesuai dengan hukum refleksi, yang menyatakan bahwa sudut datang sama dengan sudut pantul. Prinsip ini digunakan dalam perancangan lensa, cermin, dan berbagai alat optik lainnya.
Dalam kehidupan sehari-hari, kita juga sering melihat refleksi pada permukaan air, seperti genangan air atau kolam. Bayangan objek yang ada di atas permukaan air terlihat seperti terpantul di bawah permukaan, yang merupakan contoh nyata dari refleksi. Dengan memahami prinsip refleksi, kita dapat lebih memahami bagaimana cahaya dan objek berinteraksi satu sama lain.
Dengan demikian, penerapan rumus refleksi tidak hanya terbatas pada matematika, tetapi juga sangat relevan dalam berbagai aspek kehidupan sehari-hari. Pemahaman tentang refleksi membantu kita dalam memahami dunia di sekitar kita dan menerapkannya dalam berbagai situasi.



















Komentar