Varians adalah salah satu konsep penting dalam statistika yang digunakan untuk mengukur seberapa besar penyebaran data dari nilai rata-ratanya. Dalam dunia pendidikan dan penelitian, pemahaman tentang varians sangat krusial karena membantu kita memahami sejauh mana data bervariasi. Terutama ketika kita berbicara tentang “rumus varians data tunggal”, ini menjadi dasar untuk menganalisis data yang tidak memiliki frekuensi atau kelas.
Dalam konteks pendidikan, siswa sering kali kesulitan memahami bagaimana menghitung varians, terutama karena rumusnya terlihat rumit. Namun, dengan penjelasan yang jelas dan contoh soal yang relevan, setiap orang bisa memahami konsep ini. Artikel ini akan menjelaskan pengertian varians, rumus varians data tunggal, serta cara menghitungnya secara detail.
Varians data tunggal digunakan ketika kita hanya memiliki satu set data tanpa adanya kelompok atau frekuensi. Ini berbeda dengan varians data kelompok yang melibatkan kelas-kelas dan frekuensi masing-masing. Dengan memahami varians data tunggal, kita dapat mengevaluasi seberapa homogen atau heterogen suatu data. Semakin tinggi nilai varians, semakin besar variasi data tersebut, dan sebaliknya.
Artikel ini akan memberikan panduan lengkap tentang rumus varians data tunggal, termasuk langkah-langkah perhitungan, contoh soal, dan penjelasan sederhana agar mudah dipahami oleh pembaca. Selain itu, artikel ini juga akan menjelaskan perbedaan antara varians populasi dan varians sampel, serta kegunaannya dalam analisis statistik.
Apa Itu Varians?
Varians adalah ukuran statistik yang digunakan untuk mengukur seberapa besar data tersebar dari nilai rata-ratanya. Dalam istilah sederhana, varians menggambarkan sejauh mana data berbeda satu sama lain. Jika semua data memiliki nilai yang hampir sama, maka variansnya akan rendah. Sebaliknya, jika data memiliki variasi yang besar, maka variansnya akan tinggi.
Dalam statistika, varians sering digunakan untuk mengevaluasi ketidakpastian atau risiko dalam data. Misalnya, dalam bidang finansial, varians digunakan untuk mengukur volatilitas harga saham. Dalam pendidikan, varians bisa digunakan untuk mengevaluasi sejauh mana hasil ujian siswa bervariasi dari rata-ratanya.
Varians juga menjadi dasar dalam perhitungan simpangan baku (standar deviasi), yang merupakan akar kuadrat dari varians. Simpangan baku lebih mudah dipahami karena memiliki satuan yang sama dengan data aslinya, sedangkan varians memiliki satuan kuadrat.
Jenis-Jenis Varians
Terdapat dua jenis utama varians dalam statistika, yaitu:
- Varians Populasi
Varians populasi digunakan ketika kita memiliki seluruh data dari populasi yang ingin kita analisis. Dalam perhitungan varians populasi, kita menggunakan seluruh data yang ada dan membaginya dengan jumlah total data (N). Rumus varians populasi adalah:
$$
\sigma^2 = \frac{\sum (x_i – \mu)^2}{N}
$$
Di mana:
– $\sigma^2$ = varians populasi
– $x_i$ = data ke-i
– $\mu$ = rata-rata populasi
– $N$ = jumlah data
- Varians Sampel
Varians sampel digunakan ketika kita hanya memiliki sebagian data dari populasi. Dalam perhitungan varians sampel, kita membagi jumlah kuadrat selisih dengan $n-1$ (bukan $N$) untuk menghindari bias dalam estimasi. Rumus varians sampel adalah:
$$
s^2 = \frac{\sum (x_i – \bar{x})^2}{n-1}
$$
Di mana:
– $s^2$ = varians sampel
– $x_i$ = data ke-i
– $\bar{x}$ = rata-rata sampel
– $n$ = jumlah data sampel
Perbedaan utama antara kedua jenis varians ini adalah bahwa varians populasi digunakan ketika kita memiliki seluruh data, sedangkan varians sampel digunakan ketika kita hanya memiliki sebagian data.
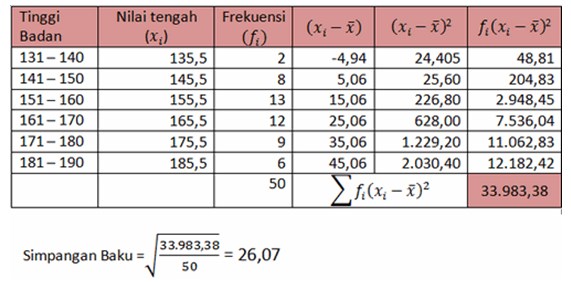
Rumus Varians Data Tunggal
Rumus varians data tunggal digunakan ketika kita hanya memiliki satu set data tanpa adanya kelompok atau frekuensi. Berikut adalah rumus umum untuk menghitung varians data tunggal:
$$
\sigma^2 = \frac{\sum (x_i – \mu)^2}{N}
$$
Di mana:
– $\sigma^2$ = varians
– $x_i$ = data ke-i
– $\mu$ = rata-rata data
– $N$ = jumlah data
Langkah-langkah untuk menghitung varians data tunggal adalah sebagai berikut:
- Hitung rata-rata data ($\mu$)
Rata-rata data dihitung dengan menjumlahkan semua data dan membaginya dengan jumlah data.
$$
\mu = \frac{\sum x_i}{N}
$$
-
Hitung selisih antara setiap data dengan rata-rata ($x_i – \mu$)
Setiap data dikurangi dengan rata-rata. -
Kuadratkan selisih tersebut ($(x_i – \mu)^2$)
Hasil dari langkah sebelumnya dikuadratkan. -
Jumlahkan semua hasil kuadrat tersebut ($\sum (x_i – \mu)^2$)
Jumlahkan semua hasil kuadrat dari setiap data. -
Bagi jumlah kuadrat dengan jumlah data ($N$)
Hasil akhir dari langkah ini adalah varians.
Contoh Soal dan Cara Menghitung Varians Data Tunggal
Berikut adalah contoh soal dan penyelesaian untuk menghitung varians data tunggal:
Contoh Soal 1:
Hitung varians dari data berikut: 4, 5, 4, 6, 4, 3, 5, 2, 3, 4.
Langkah Penyelesaian:
-
Hitung rata-rata data:
$$
\mu = \frac{4 + 5 + 4 + 6 + 4 + 3 + 5 + 2 + 3 + 4}{10} = \frac{40}{10} = 4
$$ -
Hitung selisih antara setiap data dengan rata-rata:
$$
(4 – 4) = 0 \
(5 – 4) = 1 \
(4 – 4) = 0 \
(6 – 4) = 2 \
(4 – 4) = 0 \
(3 – 4) = -1 \
(5 – 4) = 1 \
(2 – 4) = -2 \
(3 – 4) = -1 \
(4 – 4) = 0
$$ -
Kuadratkan selisih tersebut:
$$
0^2 = 0 \
1^2 = 1 \
0^2 = 0 \
2^2 = 4 \
0^2 = 0 \
(-1)^2 = 1 \
1^2 = 1 \
(-2)^2 = 4 \
(-1)^2 = 1 \
0^2 = 0
$$ -
Jumlahkan semua hasil kuadrat:
$$
0 + 1 + 0 + 4 + 0 + 1 + 1 + 4 + 1 + 0 = 12
$$ -
Bagi jumlah kuadrat dengan jumlah data:
$$
\sigma^2 = \frac{12}{10} = 1.2
$$
Hasil Akhir:
Varians dari data tersebut adalah 1.2.
Manfaat Memahami Rumus Varians Data Tunggal
Pemahaman tentang rumus varians data tunggal memiliki beberapa manfaat, antara lain:
- Mengidentifikasi Pola Data: Varians membantu kita memahami sejauh mana data berfluktuasi dari rata-ratanya. Hal ini berguna dalam pengambilan keputusan berdasarkan data.
- Evaluasi Kualitas Data: Dengan mengetahui varians, kita dapat mengevaluasi apakah data tersebut homogen atau heterogen.
- Analisis Risiko: Dalam bidang keuangan, varians digunakan untuk mengukur risiko investasi.
- Peningkatan Akurasi Analisis: Varians membantu meningkatkan akurasi analisis statistik, terutama dalam penelitian dan survei.
Kesimpulan
Varians data tunggal adalah konsep penting dalam statistika yang digunakan untuk mengukur seberapa besar penyebaran data dari nilai rata-ratanya. Dengan memahami rumus varians data tunggal, kita dapat menganalisis data dengan lebih baik dan membuat keputusan yang lebih tepat. Meskipun terlihat rumit pada awalnya, dengan latihan dan contoh soal yang relevan, setiap orang dapat menguasai konsep ini.
Dalam artikel ini, kita telah membahas pengertian varians, jenis-jenis varians, rumus varians data tunggal, dan contoh soal beserta penyelesaiannya. Dengan informasi ini, diharapkan pembaca dapat lebih percaya diri dalam menghitung varians dan memahami maknanya dalam analisis data.



















Komentar