Pahami Rumus Skala Peta dengan Mudah dan Lengkap
Dalam dunia pendidikan, khususnya di bidang matematika dan geografi, konsep skala peta sering muncul sebagai salah satu materi penting yang harus dikuasai oleh siswa. Skala peta adalah perbandingan antara jarak yang terdapat pada peta dengan jarak sebenarnya di permukaan bumi. Dengan memahami rumus skala peta, seseorang dapat lebih mudah menginterpretasikan informasi yang tercantum dalam peta, baik untuk keperluan akademis maupun praktis.
Peta merupakan alat bantu yang sangat penting dalam memvisualisasikan wilayah tertentu. Namun, karena ukuran bumi yang sangat besar, peta tidak dapat digambar secara langsung dengan ukuran asli. Oleh karena itu, peta dibuat dengan menggunakan skala, yaitu rasio antara jarak pada peta dan jarak sebenarnya. Konsep ini menjadi dasar dalam pembuatan peta dan penggunaannya dalam berbagai situasi, mulai dari navigasi hingga perencanaan wilayah.
Rumus skala peta sangat sederhana namun sangat berguna. Dengan mengetahui cara menghitung skala, seseorang dapat menentukan jarak sebenarnya berdasarkan jarak yang tertera pada peta atau sebaliknya. Selain itu, pemahaman tentang skala juga membantu dalam memahami perbedaan antara skala nominal dan skala batangan, serta bagaimana proyeksi peta memengaruhi akurasi pengukuran.
Artikel ini akan menjelaskan secara lengkap tentang rumus skala peta, termasuk contoh soal dan penjelasan langkah demi langkah. Kami juga akan membahas pentingnya skala dalam peta, serta bagaimana skala dapat digunakan dalam berbagai situasi nyata. Dengan demikian, pembaca akan memiliki pemahaman yang mendalam tentang konsep skala peta dan bagaimana menerapkannya dalam kehidupan sehari-hari.
Apa Itu Skala Peta?
Skala peta adalah perbandingan antara jarak yang terdapat pada peta dengan jarak sebenarnya di permukaan bumi. Misalnya, jika sebuah peta memiliki skala 1:50.000, maka setiap 1 cm pada peta mewakili 50.000 cm (atau 500 meter) di lapangan. Skala ini sangat penting karena tanpa adanya skala, peta tidak akan memberikan informasi yang akurat tentang jarak dan ukuran wilayah.
Konsep skala peta didasarkan pada prinsip bahwa peta adalah representasi mini dari wilayah yang lebih luas. Karena permukaan bumi melengkung, membuat peta dengan skala yang sama di seluruh area sangat sulit. Untuk mengatasi hal ini, para ahli pemetaan menggunakan berbagai jenis proyeksi peta, seperti proyeksi Mercator atau proyeksi Lambert, yang membantu meminimalkan distorsi dalam pengukuran jarak.
Ada dua jenis utama skala peta, yaitu skala nominal dan skala batangan. Skala nominal adalah angka yang menunjukkan rasio antara jarak pada peta dan jarak sebenarnya, seperti 1:100.000. Sementara itu, skala batangan adalah garis yang diberi tanda untuk menunjukkan jarak sebenarnya, biasanya terletak di sudut peta. Kedua jenis skala ini saling melengkapi dan digunakan untuk memastikan ketepatan pengukuran jarak.
Rumus Skala Peta
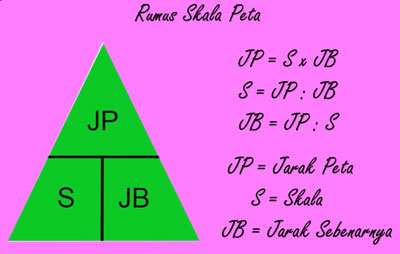
Rumus skala peta adalah dasar dalam menghitung perbandingan antara jarak pada peta dan jarak sebenarnya. Terdapat tiga rumus utama yang bisa digunakan, yaitu:
-
Rumus Skala (S)
$$
\text{Skala} = \frac{\text{Jarak pada Peta (Jp)}}{\text{Jarak Sebenarnya (Js)}}
$$ -
Rumus Jarak Sebenarnya (Js)
$$
\text{Jarak Sebenarnya} = \frac{\text{Jarak pada Peta (Jp)}}{\text{Skala (S)}}
$$ -
Rumus Jarak pada Peta (Jp)
$$
\text{Jarak pada Peta} = \text{Skala (S)} \times \text{Jarak Sebenarnya (Js)}
$$
Untuk menggunakan rumus ini, pastikan satuan jarak pada peta dan jarak sebenarnya sudah sama. Misalnya, jika jarak pada peta dinyatakan dalam sentimeter (cm), maka jarak sebenarnya juga harus dikonversi ke sentimeter. Hal ini penting agar hasil perhitungan akurat dan dapat digunakan untuk tujuan praktis.
Contoh sederhana: Jika jarak antara dua kota pada peta adalah 5 cm, dan jarak sebenarnya adalah 15 km, maka skala peta dapat dihitung sebagai berikut:
– Ubah 15 km menjadi 1.500.000 cm.
– Maka, skala = 5 cm / 1.500.000 cm = 1/300.000, atau 1:300.000.
Jenis-Jenis Skala Peta
Ada beberapa jenis skala peta yang umum digunakan, tergantung pada tujuan penggunaannya. Berikut adalah beberapa jenis skala peta yang penting untuk diketahui:
-
Skala Nominal (Skala Pecahan)
Skala nominal adalah bentuk skala yang dinyatakan dalam bentuk pecahan atau rasio, seperti 1:100.000. Ini menunjukkan bahwa 1 unit pada peta mewakili 100.000 unit yang sama di lapangan. Skala ini sangat umum digunakan dalam peta topografi dan peta umum. -
Skala Batangan (Skala Garis)
Skala batangan adalah garis yang ditempatkan di peta dan diberi tanda untuk menunjukkan jarak sebenarnya. Contohnya, garis yang panjangnya 1 cm mewakili 1 km. Skala ini sangat berguna untuk pengguna yang ingin mengukur jarak secara visual. -
Skala Titik (Faktor Skala)
Skala titik merujuk pada perubahan skala di berbagai titik pada peta. Ini sering terjadi pada peta dengan cakupan luas karena kelengkungan bumi. Untuk mengatasi masalah ini, para ahli pemetaan menggunakan proyeksi peta yang sesuai untuk mempertahankan akurasi pengukuran. -
Skala Pembesaran dan Penyusutan
Skala juga dapat digolongkan menjadi faktor pembesaran dan penyusutan. Faktor pembesaran digunakan ketika objek diperbesar, seperti dalam cetak biru bangunan. Sementara itu, faktor penyusutan digunakan ketika objek diperkecil, seperti dalam peta.
Contoh Soal Menggunakan Rumus Skala Peta
Berikut adalah beberapa contoh soal yang menggunakan rumus skala peta untuk memudahkan pemahaman:
Contoh 1: Menghitung Skala Peta
Soal:
Jarak antara kota A dan B pada peta adalah 8 cm. Jika jarak sebenarnya adalah 40 km, berapa skala peta tersebut?
Penyelesaian:
– Jarak sebenarnya = 40 km = 4.000.000 cm
– Jarak pada peta = 8 cm
– Skala = 8 cm / 4.000.000 cm = 1/500.000
– Jadi, skala peta adalah 1:500.000.
Contoh 2: Menghitung Jarak Sebenarnya
Soal:
Jika skala peta adalah 1:200.000 dan jarak antara dua titik pada peta adalah 10 cm, berapa jarak sebenarnya?
Penyelesaian:
– Skala = 1:200.000
– Jarak pada peta = 10 cm
– Jarak sebenarnya = 10 cm × 200.000 = 2.000.000 cm = 20 km.
Contoh 3: Menghitung Jarak pada Peta
Soal:
Jarak sebenarnya antara dua tempat adalah 15 km. Jika skala peta adalah 1:50.000, berapa jarak pada peta?
Penyelesaian:
– Jarak sebenarnya = 15 km = 1.500.000 cm
– Skala = 1:50.000
– Jarak pada peta = 1.500.000 cm / 50.000 = 30 cm.
Pentingnya Memahami Skala Peta
Memahami skala peta sangat penting dalam berbagai situasi, terutama dalam pengambilan keputusan yang berkaitan dengan perencanaan wilayah, navigasi, dan pengembangan infrastruktur. Dengan memahami skala, seseorang dapat menghitung jarak, luas wilayah, dan bahkan estimasi waktu tempuh antar lokasi.
Selain itu, pemahaman tentang skala peta juga membantu dalam memilih peta yang tepat untuk kebutuhan tertentu. Misalnya, peta dengan skala besar (misalnya 1:10.000) cocok digunakan untuk memetakan wilayah kecil dengan detail tinggi, sedangkan peta dengan skala kecil (misalnya 1:1.000.000) lebih cocok untuk memetakan wilayah yang lebih luas dengan detail yang lebih rendah.
Di samping itu, pemahaman tentang proyeksi peta dan perubahan skala pada peta juga penting untuk memastikan akurasi pengukuran. Proyeksi peta adalah metode yang digunakan untuk menggambar permukaan bumi yang melengkung ke bidang datar. Setiap proyeksi memiliki kelebihan dan kekurangan dalam hal akurasi skala, sehingga pemilihan proyeksi yang tepat sangat penting dalam pembuatan peta.
Kesimpulan
Rumus skala peta adalah alat penting yang digunakan untuk menghitung perbandingan antara jarak pada peta dan jarak sebenarnya. Dengan memahami konsep ini, seseorang dapat lebih mudah memahami informasi yang tercantum dalam peta dan menggunakannya dalam berbagai situasi nyata. Ada berbagai jenis skala peta yang tersedia, seperti skala nominal, skala batangan, dan skala titik, masing-masing memiliki kegunaan yang berbeda.
Dengan latihan dan pemahaman yang cukup, siapa pun dapat menghitung skala peta dengan mudah. Contoh soal yang telah disajikan di atas menunjukkan bagaimana rumus skala peta dapat diterapkan dalam situasi nyata. Dengan demikian, pemahaman tentang skala peta bukan hanya berguna dalam pelajaran matematika, tetapi juga dalam kehidupan sehari-hari.



















Komentar