Trapesium adalah salah satu bentuk bangun datar yang sering dipelajari dalam matematika. Terdiri dari empat sisi dengan sepasang sisi sejajar, trapesium memiliki berbagai sifat unik yang membedakannya dari bangun segiempat lainnya. Salah satu aspek penting dalam memahami trapesium adalah sudut-sudutnya. Setiap sudut pada trapesium memiliki karakteristik tertentu yang tergantung pada jenis trapesium itu sendiri. Dalam artikel ini, kita akan membahas secara lengkap pengertian dan sifat sudut trapesium, mulai dari definisi dasar hingga contoh penerapan dalam perhitungan matematika.
Sudut trapesium menjadi salah satu elemen penting dalam mengidentifikasi dan menganalisis bentuk trapesium. Karena trapesium memiliki dua pasang sisi yang tidak sama panjang, sudut-sudutnya juga bisa berbeda-beda. Ada beberapa jenis trapesium, seperti trapesium sama kaki, trapesium siku-siku, dan trapesium sembarang, masing-masing memiliki ciri-ciri sudut yang khas. Memahami sifat-sifat sudut trapesium sangat penting, baik untuk menyelesaikan soal-soal matematika maupun dalam penerapan nyata di kehidupan sehari-hari, seperti dalam perencanaan konstruksi atau desain arsitektur.
Selain itu, sudut trapesium juga berperan dalam rumus-rumus luas dan keliling trapesium. Dengan memahami bagaimana sudut-sudut tersebut berinteraksi dengan sisi-sisinya, Anda dapat lebih mudah menghitung nilai-nilai yang diperlukan dalam berbagai situasi. Artikel ini akan menjelaskan secara detail tentang sifat-sifat sudut trapesium, termasuk bagaimana sudut-sudut tersebut dibentuk, apa saja jenis-jenisnya, serta bagaimana mereka memengaruhi bentuk dan ukuran trapesium secara keseluruhan.
Pengertian Dasar Trapesium
Trapesium adalah bangun datar dua dimensi yang terbentuk dari empat buah sisi, di mana dua di antaranya merupakan pasangan sisi yang sejajar. Sisi sejajar ini disebut sebagai “sisi atas” dan “sisi bawah”, sedangkan dua sisi lainnya disebut sebagai “kaki trapesium”. Trapesium memiliki empat titik sudut yang saling terhubung oleh sisi-sisinya. Meskipun trapesium memiliki bentuk yang relatif sederhana, ia memiliki berbagai variasi berdasarkan panjang sisi dan besar sudutnya.
Salah satu ciri utama trapesium adalah adanya satu pasang sisi yang sejajar. Namun, sisi-sisi lainnya tidak sejajar dan dapat memiliki panjang yang sama atau berbeda. Hal ini membuat trapesium berbeda dari bangun segiempat lainnya seperti persegi, persegi panjang, atau jajar genjang. Selain itu, trapesium juga memiliki diagonal yang menghubungkan dua titik sudut yang berlawanan, meskipun panjang diagonal ini tidak selalu sama.
Pemahaman tentang trapesium sangat penting dalam bidang matematika, terutama dalam geometri. Trapesium sering digunakan dalam perhitungan luas dan keliling, serta dalam studi tentang simetri dan transformasi bangun datar. Dengan memahami struktur dasar trapesium, kita dapat lebih mudah memahami sifat-sifat sudutnya, yang akan dibahas lebih lanjut pada bagian berikutnya.
Jenis-Jenis Trapesium dan Sifat Sudutnya
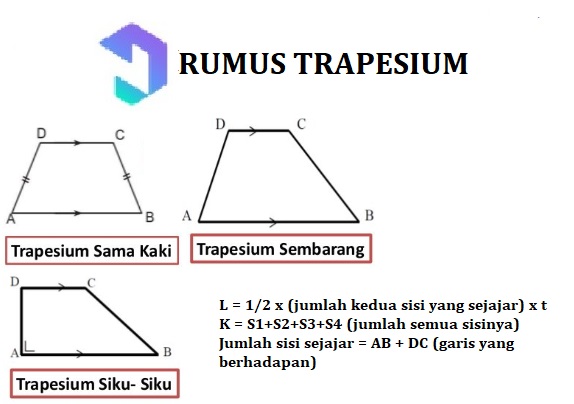
Trapesium memiliki tiga jenis utama, yaitu trapesium sama kaki, trapesium siku-siku, dan trapesium sembarang. Masing-masing jenis ini memiliki ciri-ciri dan sifat sudut yang berbeda, sehingga memengaruhi cara kita menghitung luas, keliling, dan sifat-sifat lainnya.
-
Trapesium Sama Kaki
Trapesium sama kaki memiliki dua sisi miring (kaki) yang sama panjang. Karena kedua kaki ini sama panjang, sudut-sudut yang terletak di seberang sisi sejajar juga memiliki ukuran yang sama. Misalnya, jika sisi atas dan bawah sejajar, maka sudut pada sisi atas akan sama besar dengan sudut pada sisi bawah. Selain itu, trapesium sama kaki memiliki dua diagonal yang sama panjang dan memiliki satu sumbu simetri. -
Trapesium Siku-Siku
Trapesium siku-siku memiliki dua sudut yang berbentuk siku-siku (90°). Biasanya, sudut-sudut ini terletak di ujung kaki trapesium yang tegak lurus terhadap sisi sejajar. Karena adanya sudut siku-siku, trapesium ini memiliki sifat khusus dalam perhitungan tinggi dan luas. Diagonal trapesium siku-siku tidak sama panjang, dan hanya satu sudut yang memiliki besar 90°. -
Trapesium Sembarang
Trapesium sembarang adalah jenis trapesium yang tidak memiliki sisi miring yang sama panjang dan tidak memiliki sudut siku-siku. Oleh karena itu, semua sudutnya memiliki ukuran yang berbeda dan tidak ada simetri yang jelas. Sifat sudut pada trapesium sembarang sangat variatif, tergantung pada bentuk dan ukuran sisinya.
Dengan memahami jenis-jenis trapesium dan sifat-sifat sudutnya, kita dapat lebih mudah mengidentifikasi dan menganalisis trapesium dalam berbagai situasi, baik dalam pembelajaran matematika maupun dalam penerapan nyata.
Sifat-Sifat Sudut Trapesium
Sudut-sudut dalam trapesium memiliki beberapa sifat khas yang membedakannya dari bangun segiempat lainnya. Berikut adalah beberapa sifat utama sudut trapesium:
-
Jumlah Total Sudut
Jumlah total sudut dalam trapesium adalah 360 derajat. Ini berlaku untuk semua jenis trapesium, baik itu trapesium sama kaki, siku-siku, maupun sembarang. Artinya, jumlah dari semua sudut yang ada di dalam trapesium selalu sama, terlepas dari ukuran atau bentuknya. -
Sudut Bersebelahan
Sudut-sudut yang bersebelahan dalam trapesium memiliki jumlah yang sama dengan 180 derajat. Misalnya, jika sudut A dan sudut B bersebelahan, maka jumlah keduanya adalah 180°. Hal ini terjadi karena sisi sejajar dalam trapesium membentuk pasangan sudut yang saling berpelurus. -
Sudut Pada Sisi Sejajar
Sudut-sudut yang terletak di sepanjang sisi sejajar memiliki hubungan khusus. Pada trapesium sama kaki, sudut-sudut yang berada di sisi sejajar memiliki ukuran yang sama. Sedangkan pada trapesium siku-siku, dua sudut di antara mereka adalah sudut siku-siku (90°). -
Simetri Sudut
Trapesium sama kaki memiliki simetri sumbu yang membagi trapesium menjadi dua bagian yang sama. Akibatnya, sudut-sudut yang berada di seberang sisi sejajar memiliki ukuran yang sama. Namun, trapesium siku-siku dan sembarang tidak memiliki simetri yang jelas. -
Ketergantungan pada Bentuk Trapesium
Besar sudut dalam trapesium sangat bergantung pada bentuk dan ukuran sisinya. Misalnya, pada trapesium siku-siku, dua sudut memiliki besar 90°, sedangkan pada trapesium sembarang, semua sudut memiliki ukuran yang berbeda.
Memahami sifat-sifat sudut trapesium sangat penting dalam menganalisis dan menghitung berbagai parameter trapesium, seperti luas dan keliling.
Peran Sudut dalam Rumus Luas dan Keliling Trapesium
Sudut dalam trapesium memengaruhi cara kita menghitung luas dan kelilingnya, meskipun dalam banyak kasus, sudut tidak langsung digunakan dalam rumus-rumus tersebut. Namun, pemahaman tentang sudut sangat penting untuk menentukan tinggi trapesium, yang merupakan komponen kunci dalam perhitungan luas.
Rumus Luas Trapesium
Rumus luas trapesium adalah:
$$
\text{Luas} = \frac{1}{2} \times (\text{Panjang Sisi Atas} + \text{Panjang Sisi Bawah}) \times \text{Tinggi}
$$
Tinggi trapesium adalah jarak tegak lurus antara dua sisi sejajar. Dalam trapesium siku-siku, tinggi biasanya sama dengan panjang salah satu kaki yang tegak lurus terhadap sisi sejajar. Sedangkan dalam trapesium sama kaki atau sembarang, tinggi harus dihitung menggunakan metode trigonometri atau teorema Pythagoras.
Rumus Keliling Trapesium
Rumus keliling trapesium adalah:
$$
\text{Keliling} = \text{Panjang Sisi Atas} + \text{Panjang Sisi Bawah} + \text{Panjang Kaki 1} + \text{Panjang Kaki 2}
$$
Meskipun sudut tidak secara langsung digunakan dalam perhitungan keliling, pemahaman tentang sudut membantu kita menentukan panjang sisi-sisi trapesium, terutama ketika informasi yang diberikan tidak lengkap.
Contoh Penerapan
Misalnya, jika kita diberikan trapesium dengan sisi atas 8 cm, sisi bawah 12 cm, dan tinggi 5 cm, maka luasnya adalah:
$$
\text{Luas} = \frac{1}{2} \times (8 + 12) \times 5 = 50 \, \text{cm}^2
$$
Sementara itu, jika panjang kaki-kaki trapesium adalah 6 cm dan 7 cm, maka kelilingnya adalah:
$$
\text{Keliling} = 8 + 12 + 6 + 7 = 33 \, \text{cm}
$$
Dengan demikian, meskipun sudut tidak langsung digunakan dalam rumus-rumus tersebut, pemahaman tentang sudut tetap penting dalam menentukan tinggi dan panjang sisi-sisi trapesium.
Contoh Soal dan Pembahasan
Untuk lebih memahami cara menghitung luas dan keliling trapesium berdasarkan sudut-sudutnya, berikut adalah beberapa contoh soal beserta penyelesaiannya.
Contoh Soal 1: Trapesium Siku-Siku
Sebuah trapesium siku-siku memiliki sisi atas 5 cm, sisi bawah 9 cm, dan tinggi 4 cm. Panjang kaki pertama adalah 4 cm, sedangkan kaki kedua adalah 6 cm. Hitunglah luas dan keliling trapesium tersebut.
Penyelesaian:
-
Luas Trapesium:
$$
\text{Luas} = \frac{1}{2} \times (5 + 9) \times 4 = \frac{1}{2} \times 14 \times 4 = 28 \, \text{cm}^2
$$ -
Keliling Trapesium:
$$
\text{Keliling} = 5 + 9 + 4 + 6 = 24 \, \text{cm}
$$
Contoh Soal 2: Trapesium Sama Kaki
Sebuah trapesium sama kaki memiliki sisi atas 6 cm, sisi bawah 10 cm, dan tinggi 5 cm. Panjang kaki-kaki trapesium adalah 5 cm. Hitunglah luas dan keliling trapesium tersebut.
Penyelesaian:
-
Luas Trapesium:
$$
\text{Luas} = \frac{1}{2} \times (6 + 10) \times 5 = \frac{1}{2} \times 16 \times 5 = 40 \, \text{cm}^2
$$ -
Keliling Trapesium:
$$
\text{Keliling} = 6 + 10 + 5 + 5 = 26 \, \text{cm}
$$
Contoh Soal 3: Trapesium Sembarang
Sebuah trapesium sembarang memiliki sisi atas 7 cm, sisi bawah 12 cm, dan tinggi 6 cm. Panjang kaki pertama adalah 8 cm, sedangkan kaki kedua adalah 9 cm. Hitunglah luas dan keliling trapesium tersebut.
Penyelesaian:
-
Luas Trapesium:
$$
\text{Luas} = \frac{1}{2} \times (7 + 12) \times 6 = \frac{1}{2} \times 19 \times 6 = 57 \, \text{cm}^2
$$ -
Keliling Trapesium:
$$
\text{Keliling} = 7 + 12 + 8 + 9 = 36 \, \text{cm}
$$
Dengan contoh-contoh soal di atas, kita dapat melihat bagaimana sudut dan sifat-sifat trapesium memengaruhi perhitungan luas dan keliling. Meskipun sudut tidak langsung digunakan dalam rumus, pemahaman tentang sudut sangat penting dalam menentukan tinggi dan panjang sisi-sisi trapesium.
Kesimpulan
Trapesium adalah bangun datar segiempat yang memiliki satu pasang sisi sejajar. Salah satu aspek penting dalam memahami trapesium adalah sudut-sudutnya, yang memiliki sifat-sifat khas tergantung pada jenis trapesium. Trapesium sama kaki memiliki dua sudut yang sama besar di sepanjang sisi sejajar, trapesium siku-siku memiliki dua sudut siku-siku, dan trapesium sembarang memiliki sudut-sudut yang berbeda-beda.
Pemahaman tentang sudut trapesium sangat penting dalam menghitung luas dan keliling, serta dalam menganalisis bentuk dan ukuran trapesium. Meskipun dalam rumus-rumus luas dan keliling trapesium, sudut tidak secara langsung digunakan, tinggi trapesium yang merupakan komponen kunci dalam perhitungan luas sering kali terkait dengan sudut-sudut trapesium.
Dengan memahami sifat-sifat sudut trapesium, kita dapat lebih mudah mengidentifikasi dan menganalisis berbagai jenis trapesium dalam berbagai situasi, baik dalam pembelajaran matematika maupun dalam penerapan nyata. Dengan begitu, kita tidak hanya memahami konsep trapesium secara teori, tetapi juga mampu menerapkannya dalam kehidupan sehari-hari.



















Komentar